CS641 Class 8

Building C programs: Sec. 2.12 Handout on Building a C program from two source files

prog.c --> prog.s by C compiler

---> prog.o (object file) by assembler

---> prog (executable) by linker

On UNIX, the OS exec system call loads prog into memory

SPIM: does assembly, linking, loading, so we don’t see the steps

Using MIPS cross tools (mips-gcc, etc), we can see the steps but can’t execute the result.

Using native tools (gcc), we can see the steps and run the result.

gcc –S prog.c creates prog.s

gcc –c prog.c creates prog.o

gcc prog.c -o prog creates prog (or a.out if no –o)

prog.o: an object file, assembled but not yet linked—what does that mean?

· has machine language instructions in text segment, composed data in data segment

· each segment has determined layout, for example a certain instruction is 96 bytes from the start of the code segment.

· has symbol table

· but some symbols still have unknown value, because the start address of each segment is unknown

So “jal printchar” has known form, but not known value for printchar

So prog.o has the jal and some markup about how to fix up printchar once the location is known.

Case of two .c files: see handout

Computer Components

pg. 14, more or less--

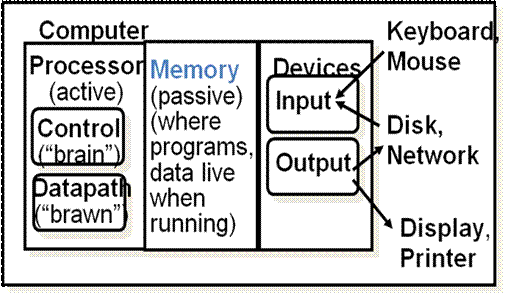
Basic Hierarchy:

° Processor

° executes instructions on order of nanoseconds to picoseconds, say 1ns for simplicity

° holds a small amount of code and data

° Memory

° More capacity, still limited

° Access time ~50-70 ns (pg. 23) (about 50 times slower than processor)

° Disk

° HUGE capacity (virtually limitless)

° VERY slow: runs on order of milliseconds (5-20 ms, pg. 23) 100,000 times slower than memory!!

Flash Memory: in between memory and disk, but wears out, a challenge to integrate properly.

Memory Caching

° We’ve discussed three levels in the hierarchy: processor, memory, disk

° Mismatch between processor and memory speeds leads us to add a new level: a memory cache

° Implemented with SRAM technology: faster but more expensive than DRAM memory.

Costs (why do we need cache)

° Memory

• SRAM .5 – 5 ns , $2000-5,000 per gb (pg. 453, 2008)

• DRAM 50-70 ns , $20-75 per gb

• Disk 5m – 20m ns, $.2-2.00 per gb

• Use a small amount of sram, make it appear to be a large amount

° If level is closer to Processor, it must be:

• smaller

• faster

• subset of lower levels (contains most recently used data)

° Lowest Level (usually disk) contains all available data

° Other levels contain copies

° When Processor needs something, bring it into to all higher levels of memory.

° Cache contains copies of data in memory that are being used.

° Memory contains copies of data on disk that are being used.

° Entire idea is based on Temporal Locality: if we use it now, we’ll want to use it again soon (a Big Idea)

° Temporal locality – if you use an item, likely to use it again

° Spatial locality- if you use an item, likely to use nearby items

Cache Design

° How do we organize cache?

° Where does each memory address map to?

(Remember that cache is subset of memory, so multiple memory addresses map to the same cache location.)

° How do we know which elements are in cache?

° How do we quickly locate them?

Direct-Mapped Cache

° In a direct-mapped cache, each memory address is associated with one possible block within the cache

• Therefore, we only need to look in a single location in the cache for the data if it exists in the cache

• Block is the unit of transfer between cache and memory

mappings

° Block number = (address ) modulo (number of blocks in cache)

° If number of blocks = power of 2 then this is easy to compute

Toy example: 1 byte blocks, 4 cache slots, 16 bytes of memory

° blockno = a mod 4. blockno = 0 if a % 4 == 0, i.e., a is a multiple of 4:

WARNING: this diagram (from Prof. Cheung’s slides) has memory addresses going down the page, rather than our usual orientation.

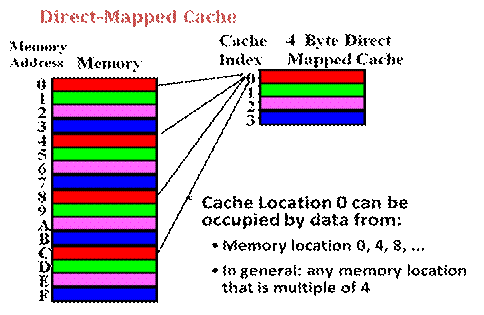
° Since multiple memory addresses map to same cache index, how do we tell which one is in there?

° Need additional bits to know the whole address – called tag bits

° How do we know if any bits are in cache – need an additional bit called valid bit

Tag bits: the “upper” bits in the address

Toy example: A = 0xb = 1011 = 10|11| block 11 = 3 , tag 10

° Entry for it in cache (entry 3): 10|dddddddd|1 (tag to start, valid bit at end)

° See entry, reconstruct A: entry 3, so index = 3 = 11, use tag from entry: A = 10|11||

Look at all 4 addresses that map to this cache slot, to see the tags doing their id work:

° A = 0011 (tag 00), A = 0111 (tag 01), A= 1011 (tag 10), A=1111 (tag 11)

Back to general case: case of multiple bytes in a block

So we need an “offset” to specify which byte in the block our specific address points to.

Note: As long as the size of the cache and the size of the block are both powers of 2, everything we need can be expressed as simple bit fields of the address. Let’s assume that. Then we look at the bits of an address, and will see the following format:

Direct-Mapped Cache Terminology

° All fields are read as unsigned integers.

° Index: specifies the cache index (which “row” of the cache we should look in)

° Offset: once we’ve found correct block, specifies which byte within the block we want

° Tag: the remaining bits after offset and index are determined; these are used to distinguish between all the memory addresses that map to the same location

Bigger Example: Suppose we have a 16KB of data in a direct-mapped cache with 4 word blocks (32-bit machine)

° Determine the size of the tag, index and offset fields if we’re using a 32-bit architecture

Solution:

° Offset

• need to specify correct byte within a block

• block contains 4 words

= 16 bytes

= 2⁴ bytes

• need 4 bits to specify correct byte

° Index: (~index into an “array of blocks”)

• need to specify correct row in cache

• cache contains 16 KB = 2¹⁴ bytes

• block contains 2⁴ bytes (4 words)

• # blocks/cache

= bytes/cache bytes/block

= 2¹⁴ bytes/cache 2⁴ bytes/block

= 2¹⁰ blocks/cache

• need 10 bits to specify this many rows

• Tag: use remaining bits as tag

• tag length = addr length – offset - index
= 32 - 4 - 10 bits
= 18 bits

• so tag is leftmost 18 bits of memory address

• Why not full 32 bit address as tag?

• Bytes within block need 4 bits offset address

• Index must be same for every address within a block. It is redundant in tag check, thus can leave off to save memory (10 bits in this example)

How big is this cache in memory? It’s holding 16KB of data, but needs tags and valid bits, 19 bits/entry, 1024 entries, so 19*1024 = 19 K extra bits, over the basic 16KB = 128 K bits, for a total of 147 Kbits = 18.4 KB (calc’d on pg. 463)

Example A= 0x12345678

Find tag, index, offset—try it!