CS641 Class 12  SMP (7.3), Cache Coherence (5.8)

after that (and after spring break): Synchronization and Mutex (2.11), then start on digital logic—see syllabus for linked doc as well as book sections.

SMP: we briefly discussed this earlier, and looked at the organization picture on pg. 639:

--each processor has its own cache, but these caches communicate (cache coherence topic)

--each processor can access the shared memory, hanging off the common bus

Important picture: To a parallel programming program, shared memory looks a lot like the program memory we have sketched for an ordinary program. We just have multiple stacks, one for each thread, instead of a single stack for the program.  Consider the case of 4 threads running in a program on a 2 core SMP system.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

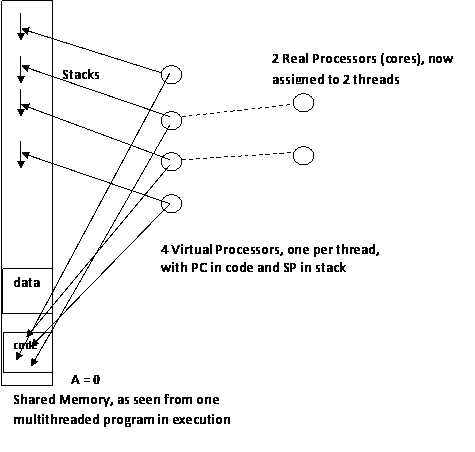
The OS runs the scheduling of the threads, assigning real processors to the virtual processors based on round robin (say) among the threads that are ready to run. When a thread needs to do i/o, it blocks (in the OS) and is no longer ready to run, so it loses its real processor. Similarly, if a thread needs to block on a mutex, that is known to the OS and also causes a thread switch.

Recall that when a program waits for memory, that is not known to the OS, and so can’t cause a thread switch. It is just lost time.

Need for mutex, short for mutual exclusion, and a form of inter-thread synchronization.

Example of counting in a certain variable C in shared memory, containing 42 initially.

What we might expect:

Thread T1 adds 1 to C: C goes from 42 to 43

Thread T2 adds 1 to C: C goes from 43 to 44

Drilling down, adding one to a location requires a read over the bus and then a write back over the bus. These reads and writes can be interleaved in a multiprocessor (or even in a multithreaded program running on a uniprocessor, but far less often.)  So we can have:

T1 reads 42

T2 reads 42

T1 writes 43

T2 writes 43

So only one increment has been recorded, instead of the expected two.  This is called the “lost update problem”.

Mutex can solve this problem. With mutex, only one thread at a time is allowed to execute a piece of code. So we have:

T1 sets mutex

T1 reads 42

T1 writes 43

T1 releases mutex

T2 sets mutex

T2 reads 43

T2 writes 44

T2 releases mutex

Note that T2 can try to set the mutex while T1 has it, but it will be forced to wait (blocked in OS), until T1 releases the mutex.

Example of enqueue

An enqueue operation takes a few reads and writes of pointers to do its work.  If two enqueues are interleaved, the data structure can be corrupted. The solution again is to use a mutex and force the enqueues to happen one-by-one.

It turns out that we need help from the hardware to make a foolproof mutex.  We’ll be looking at Sec 2.11 soon about special instructions for this.

Sample program in the book, pg. 639

100000 numbers to add up on 100 processors.

Basic idea here: each processor adds up 1/100 of the numbers. Then the sub-sums are added up.

This will not speed up well at all. The job is way too memory intensive. The progress of the threads will be limited to the memory bandwidth to the shared memory, which can probably be saturated by 3 processors running in such a tight loop.

We need jobs where each processor can read a little bit of memory and then do significant work on its own.  Ray tracing is like that, and a lot of other real applications. A simple example is the Mandelbrot fractal image.

Example of MandelbrotFractal.java, handed out (uses 10 threads, each calculating 1/10 of the pixels)

Consider a 1000x400 image, so 400,000 pixels to calculate.

To determine the color of each pixel of a Mandelbrot image, a loop has to be done.  We want to see that this code doesn’t access shared memory very much.

First we look at the global variables: img, pix, w, h, alpha.

The thread code is in run(). There is a bunch of local variables defined for it. These live on the thread stack, private to the thread. The local var imax is initialized from w*h, accessing global variables.

The i-loop is the loop across the pixels. Inside the i-loop, there is another loop from 0 to 255. This is the computation for a single pixel, with doubles (x,y) calculated based on previous (x,y) until the (x,y) flies out of a certain circle. The number of steps needed to reach this point is the result that determines the color.

But we don’t need to understand the details here, as we are looking for access to shared memory. All these variables are local except alpha and pix, and these are only accessed when the loop is being finished up, so once each.

The accesses to global variables w, h, and alpha are reads only, so these values get put in the processor cache on first access and stay there, so cost only one read per processor, a trivial load.

The access  pix[w*ky+kx] = val is a write to shared memory.  One of these happens for each pixel.

Note: there are some expressions in this code that are more complicated than necessary. I want to show that pix[w*ky + kx] is just pix[i].

First note that kx = i%w and ky = (i-kx)/w by assignments.  Note this is integer arithmetic.

So   ky = (i – i%w)/w.  Here i - i%w  is i rounded down to a multiple of w, so (i-i%w)/w is the number of w’s that fit in i, which is exactly what i/w is.  So ky = i/w.

Watch out here: integer arithmetic is tricky. It is not true in general that (x – y)/w = x/w – y/w.  Consider that (12-7)/6 = 0 but 12/6 – 7/6 = 2 -1 = 1.  We had to argue more carefully!

So pix[w*ky + kx] = pix[ w*(i/w) + i%w] = p[i]   since w*(i/w) = i rounded down to a multiple of w, and i%w is the rounded amount.

So it is now easy to understand the i-loop’s action.  Each value of i runs the inner loop and sets pix[i].

Consider the i-loop control

                 for (i=k; i<imax; i += maxThr)

Here imax = # pixels = 400000, and maxThr = 10.  k is the thread id, k=0, 1, ..., 9, set up by the constructor.

Consider thread 3, so k=3. It executes     

for (i=3; i<400000; i += 10)

i.e., i = 3, 13, 23, ... , 399993,  every 10^th value of i

So this sets pix[3], pix[13], pix[23],...pix[399993]

While thread 4 does pix[4], pix[14], pix[24],...pix[399994]

If we look at the pix array in memory, we know it will be brought into caches by cache lines, which may be 8 words long (say), and each cache line will be accessed by 8 different threads running on different processors in the interesting case.

This is an expensive way to do it.  A cache line will be read into various caches, get written on by other processors, written back out, etc.

All we have to do to improve this code is split up the array by 1/10ths and have each thread work on its part of the array.

Each thread does imax/maxThr pixels in a row, from k*(imax/maxThr) to (just short of) (k+1)*(imax/maxThr)

                for (i= k*(imax/maxThr) , i < (k*1)*(imax/maxThre); i++)

Now, except on the edges of the regions, each cache line will be in only one processor cache, and will be written on there until done, and written out somewhat later (write back cache assumed).

We see that writing good parallel code is non-trivial even when we have such a highly parallelizable situation as this. Actually, in fact we have not shown that memory access time is important to this computation.

Experimental results

1000x400 Mandelbrot image created by MandelbrotFractal, running on 2 processors on Windows XP

This output was captured from the “Java Console” started from the Java toolbar icon.

Number of threads: 1

Run Time in Millis: 172

Number of threads: 2

Run Time in Millis: 63

Number of threads: 10

Run Time in Millis: 78

This shows overly good speedup with 2 threads. We should run the first case twice and discard the very first case as a warmup.

Rerun with two runs with 1 thread: the second run at 1 thread is significantly faster:

Number of threads: 1

Run Time in Millis: 188

Number of threads: 1

Run Time in Millis: 125

Number of threads: 2

Run Time in Millis: 78   

Number of threads: 10

Run Time in Millis: 78

Cache Coherence: Sec. 5.8

Look at Fig. 5.35, and see the base situation that is leading up to problems: after A stores X, B’s cache has a stale value.

Will a subsequent read by B get the wrong value?

Well, if stale values are allowed to hang around for significant time and are then used, it’s a real problem. It turns out that we tolerate a little bit of staleness for performance sake.  After all, the threads on different processors are not synchronized unless we ask for special synchronization.

Look at the rules on pg. 535.

I’ll write them in database notation: w1(x) means write by processor 1 on data item x.  r2(x) is a read of x by processor 2.

1.       w1(x) r1(x): the read must return the value previously written by the same processor

2.       w2(x) r1(x) with no w(x)’s between: returns the written value to the read if the w and r are close enough in time

3.       w1(x)w2(x) can be done out of order, but whatever order of writes seen by one processor must be seen by all—this is the “serialization order” chosen by the system. 

What this is aiming at is a good story about what happened to an x value in observable memory. No processor can see a different succession of values in x from another processor. It has to act like a uniprocessor on reads and writes it does for its own programs.

How can a system keep even this much order?  Snooping protocols on buses are the most common way.  A bus has address lines, a R/W line, and for a multiprocessor, lines for the processor id doing the current bus cycle (read or write).  All the caches are connected to this common bus, so they can interpret all the reads and writes of the other caches. Also, they can use the bus to talk to other caches.

So in the situation of Fig. 5.35, cache A does a write of X and can notify all other caches of this (using the bus), and B can remove the stale entry.