CS110 Project 3

Bob Wilson

Writing a Class “from Scratch” to Satisfy a Provided API and JUnit TestCase

Some applications involve linear equations such as:

ax + by = c

These algebraic “lines” are modeled as “objects” in an Object-Oriented Programming strategy. Hence, we need a class named Equation that can be used to create linear equations and solve pairs of them for X and Y. In this project, you will write a class that supports linear equations and solving pairs of linear equations. It will also implement the Comparable interface. Study the java.lang.Comparable interface and the java.util.Arrays class and its static sort method on the Sun Java website.

I have provided a Project3.zip with a JUnit TestCase class that you can use to test your Equation class. Unzip the directory and setup a Dr Java project. In your Dr Java project, create/save a new source file named Equation.java and write your code in it, compile it, and test the project. Keep testing the project until the code for your Equation class passes all the test cases (shows all green).

The UML class diagram for the whole project is shown in this figure:

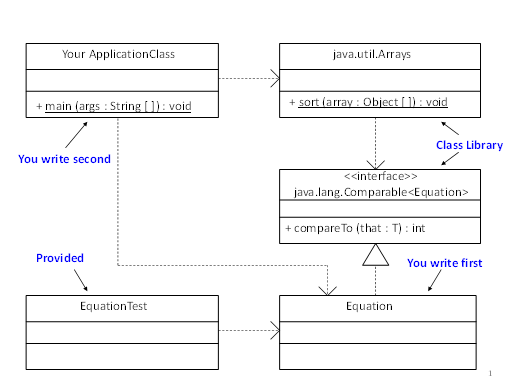
The detailed UML class diagram describing the API for the Equation class is provided here.

Equation implements Comparable<Equation>

+ THRESHHOLD : double // threshold for comparisons of double values

- a : int // coefficient of the variable x

- b : int // coefficient of the variable y

- c : int // constant

+ Equation(a : int, b : int, c : int) // constructor

+ toString( ) : String // return a String representing the equation

+ slope( ) : double // return the slope of the line

+ intercept( ) : double // return the y-axis intercept of the line

+ compareTo(that : Equation) : int // compare values of equations

// solving methods for pairs of equations:

+ solveForXWith(that : Equation) : double // solve for X

+ solveForYWith(that : Equation) : double // solve for Y

+ verifySolution(x : double, y : double) : boolean // verify correct

The Equation class encapsulates four attributes:

1. A public class constant named THRESHHOLD that can be used for comparisons of double values such as return values from the slope and intercept methods. This constant will also be used in the code of the Equation class methods when comparison of double components is required such as in the implementation of the compareTo method. A reasonable value for this constant is 0.001. In code outside of the Equation class, it can be accessed as Equation.THRESHHOLD. In code inside the Equation class, it can be accessed simply as THRESHHOLD.

2. Three private instance attributes that represent the coefficients of the linear equation being encapsulated. The class is defined to be immutable. That means that there are no mutator or “setter” methods so the coefficent values cannot be changed after being initialized by the constructor.

Code outside of your Equation class can do the following:

1. Create Equation objects by calling the Equation constructor with three coefficients as arguments, for example:

// create an Equation object to represent: 2x + 3y = 6

Equation myEquation = new Equation(2, 3, 6);

2. Display Equation objects using the toString method, for example:

// print an Equation

System.out.println(myEquation.toString());

3. Get the slope or y-axis intercept for the equation, for example:

// print the slope and intercept for an Equation

System.out.println(myEquation.slope());

System.out.println(myEquation.intercept());

4. Compare Equation objects using the compareTo method, for example:

// compare two equations

if(myEquation.compareTo(yourEquation) < 0)

valid Java statement for when mine is less than yours;

5. Solve a pair of Equations and verify the solution, for example:

// solve a pair of Equations for X (or Y)

double x = myEquation.solveForXWith(yourEquation);

Notice that after code outside of the Equation class creates an Equation object with a given set of coefficients, it does not ever need to access the coefficient values again. So there is no need for accessor or “getter” methods to get the values of individual coefficients. All operations using the coefficients of Equation objects are done in the code of the Equation class methods, for example:

// part of compareTo - compare the slopes of two objects

double difference = this.slope() – that.slope();

The methods of the Equation class should be implemented as follows:

The constructor should initialize the coefficients a, b, and c, from the supplied parameters.

The String returned to represent an equation is a properly sequenced concatenation of the coefficients, and a couple of string literals. Study the tests of the toString method in the JUnit TestCase code to determine the proper concatenation sequence.

The slope of the line represented by the equation is calculated and returned as the negative of the coefficient a divided by the coefficient b. However, if the coefficient b is equal to zero, the slope is infinite (divide by zero) and your code should throw an ArithmeticException with the text “Infinite Slope”.

The intercept of the line represented by the equation is the value of y where it crosses the y axis (x = 0). It is calculated by dividing the coefficient c by the coefficient b. If the coefficient b is equal to zero, there is no unique value for the intercept (divide by zero) and your code should throw an ArithmeticException with the text “No Unique Intercept”.

The compareTo method is required to implement Comparable<Equation>. Comparing two equations is done by comparing their slopes. The Equation object with the larger value for its slope is larger. (This is an arbitrary definition for ordering of Equation objects and is made only to have a defined rule for implementing the Comparable interface.) The return value is an int value: zero if they are equal, i.e the absolute value of the difference in slopes is less than THRESHHOLD, minus one if “this” is smaller than “that”, and plus one if “this” is larger than “that”. NOTE: When you need the slope for calculations in this method, call the slope methods. Don’t re-type or copy-and-paste the code for calculating the slope.

The methods implementing solve for X or solve for Y with pairs of equations should operate on the coefficients of “this” Equation with the coefficients of “that” Equation using this method signature for solveForXWith:

public double solveForXWith(Equation that); // “that” is not a reserved word

Calculate the value of X or Y for a pair of equations, as follows:

Calculate the denominator for either expression as:

denominator = a_this x b_that - a_that x b_this

Calculate the appropriate numerator to solve for X as:

numerator = b_that x c_this - b_this x c_that

OR

Calculate the appropriate numerator to solve for Y as:

numerator = a_this x c_that - a_that x c_this

Check for the ArithmeticException cases and either throw an exception with the appropriate text or return the result of the division.

Again, in the calculations for solving for X or Y, there are possible divide by zero cases. If the denominator of the expression is zero and the numerator of the expression is also zero, the equations represent two overlapping lines(or an infinite number of intersections) and the code should throw an ArithmeticException with the text “Overlapping Lines”. If the denominator is zero but the numerator is not zero, the equations represent parallel but not overlapping lines (there is no solution for their intersection) and your code should throw an Arithmetic exception with the text “Parallel Lines”. Otherwise, the X or Y value is the result of the expression evaluation which should be returned.

The verifySolution method verifies that the equality represented in the equation is correct with the provided x and y parameter values. It returns a value of true if the solution is correct within the tolerance and false otherwise.

Notes: Since the coefficients a, b, and c are int and most results are double, you need to use a cast or promotion in expressions as needed to produce a double result without integer truncation during any division operations. Also, you must not compare double values with each other for equality (==) or inequality (!=). Check that the absolute value of the difference between the double values is less than the symbolic constant THRESHHOLD.

Since there is a provided test case class, you may want to fill in all the method signatures with no method code inside the { } to be able to compile and run the test cases while you write and test your code. If the method has a return type, you need at least a return statement with a suitable default value.

Documentation

Include Javadoc comments in your Equation class code with @author and @version for the class and with @param and @return for each method. In the comments for each method, include a brief description of the calculation that your code performs. Run javadoc on your Equation class file to create a webpage describing the API to your Equation class. Include a copy of this javadoc generated webpage in your project folder.

Application Class

Use the javadoc webpage for the Arrays class and your Equation class as guidance while you are writing the code for this class. You should find it easy to create and do operations on Equation objects including solving or sorting an array of them without knowing anything about the mathematics involved or the process of sorting.

Write an application class with a name of your own choosing and a main method that instantiates an Equation array containing at least 5 different Equation objects with coefficient values of your own choosing. (However, be sure that the values that you choose are not in proper sorted order for the following code to show the difference before and after sorting.) Use the solveForXWith and solveForYWith methods on two of these equations and print out the results along with the logical and of the two boolean values returned by their verifySolution methods. Then, print the contents of the array with the toString and slope values, call the Arrays.sort() method passing the array name, and print the contents of the array with the toString and slope values again.

Sample Output

> java <name of application class here>

x = 2.142857142857143, y = 0.42857142857142855, Valid Solution?: true

Before sorting:

1x +2y = 3: -0.5

-2x +10y = 0: 0.2

1x +5y = 2: -0.2

-4x +1y = 7: 4.0

1x +10y = 0: -0.1

After sorting:

1x +2y = 3: -0.5

1x +5y = 2: -0.2

1x +10y = 0: -0.1

-2x +10y = 0: 0.2

-4x +1y = 7: 4.0

>

Report (memo.txt)

For this project and all projects in this course, the memo.txt file that you upload to the turn-in system MUST BE A PLAIN TEXT FILE - NOT A WORD (.DOC or .RTF) FILE. On a Windows PC, I recommend that you use Notepad to create this file. On a MAC, you must use a suitable editor to create a plain text file.

Write a report that answers the following questions:

1. Why is it a good idea to choose names like solveForXWith, etc. for the methods that solve pairs of equations?

2. Why is it a good idea to use the slope method in the calculations for one of the other methods?

3. Was it helpful to have the provided TestEquation class while writing the code in your Equation class? Why?

4. Did the javadoc webpage for your Equation class help you to write your application class at the end? How?

Turning in your Assignment:

Use the secure file transfer program to upload your Project3 folder containing your Java source files and memo.txt file to your UNIX file directory: “account/cs110/Project3” where “account” is your account ID.

You must upload the files to our UNIX system before the posted deadline. You will get no credit for late submissions. Plan your time carefully so that you have enough time to upload your files. If you have not finished, upload your files on time anyway - even if the program does not work correctly yet. That way you are eligible for part credit on the assignment. If you upload your files more than once, only the most recent copy will be saved.