CS210 Lab 2
Bob Wilson
Solving Quadratic Equations
We want to write and test a program for solving a quadratic equation of the form:
a x2 + b x + c = 0
for
Fortunately, there is a formula that gives us
x = (-b + square root (b2 – 4ac))/2a
We can use this formula as part of the algorithm in our program to solve quadratic equations. An algorithm defines the steps in logic and calculation used for solving a problem.
There are different cases where the calculation of the above expression is impossible because some law of Mathematics is violated such as trying to take the square root of a negative number or trying to divide by zero. A complete algorithm for solving quadratic equations must include needed logic decisions based on the input values as well as calculations using different formulas.
Based on the if statement and the else clause, you have the knowledge that you need to write a good program for solving quadratic equations. Naturally, your program must properly select and execute the correct calculation for any supplied values of a, b, and c. However, here are six test cases that each force your program to select one of the six different possible calculations with the format of the solution that your program should provide for that case.
|
Value for a |
Value for b |
Value for c |
Solution for some possible test cases Should return exactly this string in each case! |
|
1 |
0 |
-3 |
Root 1 is 1.7320508075688772 Root 2 is -1.7320508075688772 |
|
1 |
1 |
1 |
Root 1 is -0.5 + i * 0.8660254037844386 Root 2 is -0.5 - i * 0.8660254037844386 |
|
1 |
2 |
1 |
The only root is -1.0 |
|
0 |
2 |
4 |
The only root is -2.0 |
|
0 |
0 |
6 |
No |
|
0 |
0 |
0 |
Any |
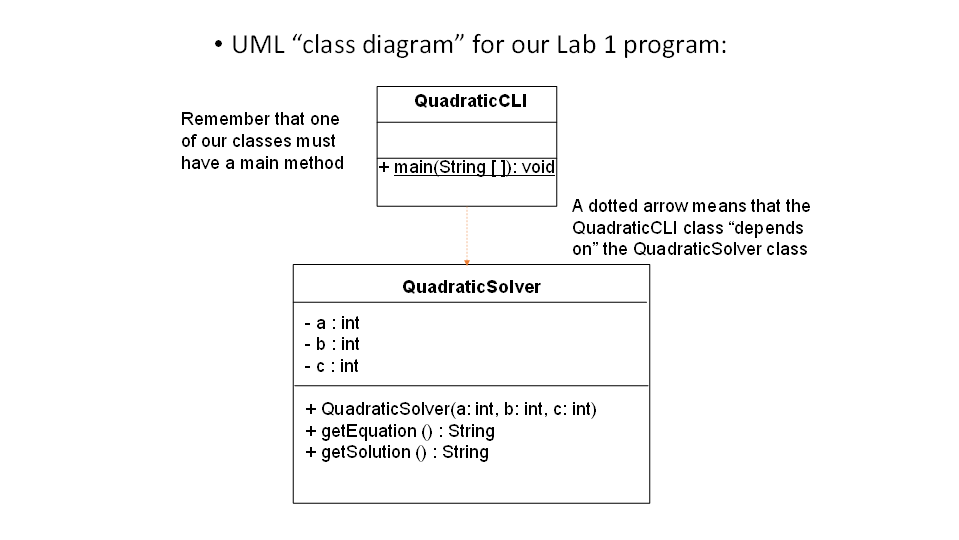
Following good OOP design principles, I have factored our solution into two classes:
A QuadraticCLI class that handles all the user input and output
A QuadraticSolver class the handles all the logic decisions and calculations
You can get the beginning project files by downloading and unzipping the following file Lab02.zip. You will be adding your code to one of the Java files in this project. Here are some things to consider:
Overall:
You must write comments in your code to document the design of your program. For this assignment, these comments must be written using the Java style single line comment by beginning a comment line with // or putting // and a comment at the end of a line of code. At a minimum, you must have appropriate comments in the method you write. Try to make these comments useful to the programmer who will be reading them and not just an English re-statement of the contents of the line(s) of code.
QuadraticCLI:
You should read the Quadratic CLI source code to understand what it is doing, but you will not need to modify it.
1. QuadraticCLI contains the main method that is the starting point for the execution of the program. You need to configure the Dr Java project configuration with the name of the class that contains the main method (QuadraticCLI) to run your program.
2. Notice that there are no calculations done in the QuadraticCLI class. The code in QuadraticCLI just stores the values of the coefficients. This class instantiates a Scanner object, uses the Scanner object to get the coefficient values, passes these values as arguments to the appropriate methods of the QuadraticSolver class, and prints the Strings returned by the QuadraticSolver class’s getEquation and getSolution methods.
Notice how the QuadraticCLI class asks the user a yes/no question and makes a decision based on the response. It prompts the user with a question and uses the Scanner method getNext to get a String input, uses a Boolean logic expression as the condition for the loop to check the response for equality with an expected response such as “yes” or “y”, and controls the flow of the program based on the condition. Note: The code uses the charAt method of the String response from scan.next() to get the first (zeroth) character and checks that character for equality (==) with the character literal ‘y’. If it were to try to match the String it would need to use the String class equals method instead of the == operator.
Also, notice which statements need to be re-executed and which do not. It does not need to re-execute the creation of the Scanner object. Therefore, it does not include that statement inside the scope of the loop.
QuadraticSolver:
1. The QuadraticSolver class does not need to have a main method.
2. The QuadraticSolver class should not use any System.out.println or any Scanner methods. It gets the values of the coefficients via parameters in its method calls. Its getEquation and getSolution methods provide a String object as their return values. The caller (e.g. QuadraticCLI) takes responsibility for displaying those strings to the user in some way that is not known to the QuadraticSolver class. Because we have not programmed any user input or output functions in the QuadraticSolver class, we can reuse our QuadraticSolver code with a different type of user interface class such as a GUI instead of a CLI at another time.
3. In the logic that you program, you should try to use the minimal number of logic checks to determine which version of the solution your code must calculate and return. This will make your program easier to read than if you use repetitive decision logic steps. You should use nested if-else statements to minimize the number of times that your code evaluates Boolean expressions. Before writing the code, think about a logical order for your code to make the needed flow of control decisions. Also, your code should not calculate the value of the discriminant until the flow of control logic determines that the value will be needed. This avoids wasting time on unneeded computations.
4. When we calculate the discriminant, we want to create an int value so that we can evaluate boolean expressions using >, <, and/or ==. Use the expression b*b - 4*a*c to calculate the discriminant to produce an int value rather than the Math.pow method which would produce a double value. If you calculate the discriminant as an integer, then you can make Boolean decisions based on the value of the discriminant without concern for a double value being almost equal to zero but not quite zero.
Lab Report:
In your own words describe your strategy for the design of the QuadraticSolver decision logic. Did you consider any other ways to do it? Why did you choose to do it the way you finally did it?
Turning in your Lab Report:
Turn in your lab report to your TA at your next lab session. Include a copy of your code.