ON THE PERFORMANCE IMPACT OF FAIR SHARE SCHEDULING
Ethan Bolker
BMC Software, Inc
University of Massachusetts, Boston
Yiping Ding
BMC Software, Inc
Fair share scheduling is a way to guarantee application performance by explicitly allocating shares of system resources among competing workloads. HP, IBM and Sun each offer a fair share scheduling package on their UNIX platforms. In this paper we construct a simple model of the semantics of CPU allocation for transaction workloads and report on some experiments that show that the model captures the behavior of each of the three implementations. Both the model and the supporting data illustrate some surprising conclusions that should help administrators to use these tools wisely.
1. Introduction
As midrange UNIX systems penetrate the server market they must provide packages that allow an administrator to specify operational or performance goals rather than requiring them to tinker with priorities (UNIX nice values). It's then the software's responsibility to adjust tuning parameters so that those goals are met, if possible. Mainframe systems have been equipped with such tools for a long time. Recently HP, IBM and Sun have introduced similar UNIX offerings in this area. HP’s Process Resource Manager for HP-UX (PRM), IBM’s Workload Manager for AIX (WLM) and Sun’s System Resource Manager for Solaris (SRM) packages each allow the administrator to specify the share of some UNIX resource like CPU or memory that should be made available to particular groups of users or processes.
In this paper we explore the semantics of packages like these, focusing on the allocation of CPU shares. We will model the behavior of share allocation, make predictions based on our model and see how the predictions match the outcome of some benchmarking experiments.
Note that share allocations are not truly performance oriented. Administrators would prefer to specify response times or throughputs and have the system determine the shares and hence the dispatching priorities . But specifying shares is a big step in the right direction. Predicting the result of setting shares is easier than predicting the result of setting priorities – once you understand some of the surprising subtleties of share semantics and their implications.
A useful side effect of the decision to employ one of these scheduling packages is the need to decide how to organize the work on your system in order to allocate resources. That very effort will help you characterize your workloads before you have even begun to tune for performance. All three packages allow you to group work by user. PRM and WLM allow you to group it by process/application as well. The packages themselves provide some reporting tools that allow you to track resource consumption for workloads you specify.
2. CPU-bound Workloads
We start our study with CPU-bound workloads since they are the easiest to understand. Suppose the system supports two workloads, each of which is CPU-bound. That is, each would use 100% of the processor’s cycles if it were permitted to do so, but the system has been configured so that the workloads are allocated shares ![]() and
and ![]() of the processor. We represent shares as fractions (normalized), so that
of the processor. We represent shares as fractions (normalized), so that ![]() . Then each workload runs on its own virtual CPU with an appropriate fraction
. Then each workload runs on its own virtual CPU with an appropriate fraction ![]() of the total processing power. Thus work which would complete in
of the total processing power. Thus work which would complete in ![]() seconds on a dedicated processor will take
seconds on a dedicated processor will take ![]() seconds instead. If we imagine that a workload consists of a stream of CPU-bound jobs with batch scheduling so that one starts as soon as its predecessor completes then we can restate this conclusion in terms of throughput: a throughput of
seconds instead. If we imagine that a workload consists of a stream of CPU-bound jobs with batch scheduling so that one starts as soon as its predecessor completes then we can restate this conclusion in terms of throughput: a throughput of ![]() jobs per second on a dedicated machine becomes
jobs per second on a dedicated machine becomes ![]() jobs per second when the workload has fraction
jobs per second when the workload has fraction ![]() of the processor. Sun and IBM verified this prediction to validate their implementations.
of the processor. Sun and IBM verified this prediction to validate their implementations.
3. Transaction Processing Workloads
In transaction processing environments a workload is rarely CPU-bound. It is usually a stream of jobs with a known arrival rate ![]() (jobs per second) where each job needs
(jobs per second) where each job needs ![]() seconds of CPU service. Then the throughput is the arrival rate, as long as the utilization
seconds of CPU service. Then the throughput is the arrival rate, as long as the utilization ![]() is less than 1 (100%). The important performance metric is the response time. With reasonable randomness assumptions for both arrival rates and service times (
is less than 1 (100%). The important performance metric is the response time. With reasonable randomness assumptions for both arrival rates and service times (![]() and
and ![]() are both averages, after all) the average response time at a uniprocessor CPU will be
are both averages, after all) the average response time at a uniprocessor CPU will be ![]() . So, for example, a 3 second job will take 3/(1-0.75) = 12 seconds (on average) on a CPU that’s 75% busy.
. So, for example, a 3 second job will take 3/(1-0.75) = 12 seconds (on average) on a CPU that’s 75% busy.
Suppose that the system supports two transaction processing workloads. Workload ![]() has CPU share
has CPU share ![]() , arrival rate
, arrival rate ![]() and service demand
and service demand ![]() , where
, where ![]() = 1, 2. What are the response times of the workloads, assuming that
= 1, 2. What are the response times of the workloads, assuming that ![]() , so that all the work can get done?
, so that all the work can get done?
The answer depends on the semantics of share assignment. There are two possibilities: shares may be caps or guarantees.
3.1. Shares as Caps
When shares are caps each workload owns its fraction of the CPU. If it needs that much processing power it will get it, but it will never get more even if the rest of the processor is idle. These are the semantics of choice when your company has a large web server and is selling fractions of that server to customers who have hired you to host their sites. Each customer gets what he or she pays for, but no more. This situation is easy to model. As before, each workload has a virtual CPU whose power is the appropriate fraction of the power of the real processor. Then a transaction workload allocated fraction ![]() of the processor will need
of the processor will need ![]() seconds to do what would take
seconds to do what would take ![]() seconds on the full machine. The utilization of the workload's virtual machine will be
seconds on the full machine. The utilization of the workload's virtual machine will be ![]() and transaction response time at the CPU will be
and transaction response time at the CPU will be ![]() , provided
, provided ![]() is less than
is less than ![]() : when shares are caps a workload’s share must exceed its utilization if it is to get its work done
: when shares are caps a workload’s share must exceed its utilization if it is to get its work done
This simple analysis helps us make our first counterintuitive assertion: share is not the same as utilization. A workload may be allocated 70% of the processor even though on the average it uses only 20%. In that case its response time will be s/(0.7-0.2) = 2s rather than the s/(1-0.2) = 1.25s it would enjoy if it owned the entire processor.
3.2. Shares as Guarantees
The situation is more complicated when shares are merely guarantees. Suppose there are two workloads each of which has been allocated a share of the CPU. Then on the average they will receive CPU time slices in the ratio ![]() whenever both are on the run queue simultaneously. But when either workload is present alone it gets the full processing power. Thus shares serve to cap CPU usage only when there is contention from other workloads. This is how you might choose to divide cycles between production and development workloads sharing a CPU. Each would be guaranteed some cycles, but would be free to use more if they became available.
whenever both are on the run queue simultaneously. But when either workload is present alone it gets the full processing power. Thus shares serve to cap CPU usage only when there is contention from other workloads. This is how you might choose to divide cycles between production and development workloads sharing a CPU. Each would be guaranteed some cycles, but would be free to use more if they became available.
In this case utilizations may be larger than shares. If workload 1 needs 70% of the cycles while workload 2 needs 10% then over time the CPU will be 80% busy. Both workloads can get their work done even if they are allocated shares![]() = 0.2 and
= 0.2 and ![]() = 0.8, since most of the time when workload 1 needs the CPU workload 2 will be absent, so workload 1 can use more than its guaranteed 20%. Allocating a small share to a busy workload slows it down but does not prevent it from completing its work, as long as the system is not saturated. But how much will it be slowed down? What will the response times be? To answer that question we propose a model for how the CPU might choose jobs from the run queue.
= 0.8, since most of the time when workload 1 needs the CPU workload 2 will be absent, so workload 1 can use more than its guaranteed 20%. Allocating a small share to a busy workload slows it down but does not prevent it from completing its work, as long as the system is not saturated. But how much will it be slowed down? What will the response times be? To answer that question we propose a model for how the CPU might choose jobs from the run queue.
Our model interprets shares as probabilities. We assume that the processor chooses to award the next available cycle to workload ![]() with probability
with probability ![]() , making that choice without looking first to see whether that workload is on the run queue at the moment. If it’s not, the cycle goes to the other workload if it is ready. If neither workload is on the run queue, the cycle is wasted. Thus we can say that in this model workload 1 runs at high priority with probability
, making that choice without looking first to see whether that workload is on the run queue at the moment. If it’s not, the cycle goes to the other workload if it is ready. If neither workload is on the run queue, the cycle is wasted. Thus we can say that in this model workload 1 runs at high priority with probability ![]() and at low priority with probability
and at low priority with probability ![]() . With the usual assumptions about random arrival rates and service times the workload response times can be computed with simple formulae.
. With the usual assumptions about random arrival rates and service times the workload response times can be computed with simple formulae.
workload 1 response time at high priority
![]() ,
,
workload 1 response time at low priority
![]() ,
,
where ![]() and
and ![]() are the utilizations of the two workloads.
are the utilizations of the two workloads.
The response time of the transactions in each workload is the weighted average of the response time when it has high priority and that when it has low priority:
workload 1 response time
![]() .
.
It’s no surprise, but worth noting, that each workload’s response time depends on both utilizations as well as on the relative shares. We will return to this point later.
4. Model Validation
How any particular operating system awards CPU time slices so that each workload gets its proper share is both subtle and system dependent. For example, SRM monitors recent activity in order to maintain the required shares over time. We do not take up those matters in this paper. We are interested in modeling the long-term average behavior of the system, not the means by which it maintains those averages.
We tested our model in several benchmark experiments. A lightweight server daemon runs on the machine to be measured. At random times a client program running on another machine asks the daemon to execute a CPU intensive job for a particular user for a random length of time. The daemon keeps track of the CPU resources that job consumes, and timestamps its start and end. A postprocessor computes utilizations and response times.
In the first set of experiments we created two transaction workloads, using a seeded random number generator so that we could see how the same job streams responded under different share allocations. Workload 1 kept the CPU about 24% busy, workload 2 about 47% busy. Figure 1 shows the average response time on our Sun system for workload 1 executing a transaction that consumes 1 second of CPU (on average) as a function of the relative share allocated to that workload. The straight line shows the response times predicted by our model.
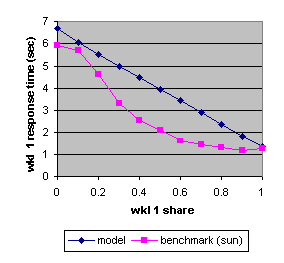
Figure 1. The benchmark and predicted average response times (Sun) of workload 1 as a function of its allocated share.
Figure 2 shows both benchmark and predicted results for the average response times for workload 2 as a function of the share allocated workload 1.
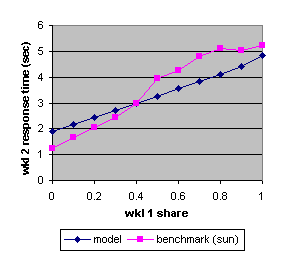
Figure 2. The benchmark and predicted average response times (Sun) of workload 2 as a function of the share allocated to workload 1.
Figure 3 shows the response times for both workloads and the average response time, weighted by workload utilization. In this case workload 2 has roughly twice the weight of workload 1. That average is nearly constant, independent of the relative share allocation, confirming the theoretical analysis that predicts response time conservation: a quantification of the fact that there’s no such thing as a free lunch. One workload only benefits at the other’s expense.
The results for HP/PRM and IBM/WLM are similar; we show them in an appendix.
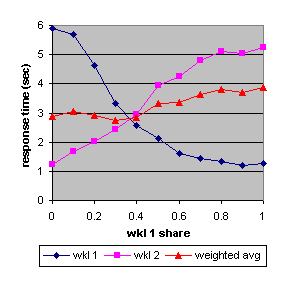
Figure 3. The measured response times (Sun) of workload 1 and workload 2 as a function of the relative share allocated to workload 1 together with their average, weighted by their utilizations
.5. Consequences
Now that we have a valid model we can explore some of the consequences of fair share CPU scheduling without having to run more benchmarks. This is exactly the kind of what if analysis models make easy.
Suppose that we imagine that the two workloads in our benchmark each grow at the same rate, so that the overall CPU utilization grows from 70% to 90%. What effect will share allocations have at these utilizations? Figure 4 tells us the answers. We have already seen the two lower lines in that figure: they come from the model corresponding to our benchmark experiment. The two upper lines represent our what if analysis.
At the higher utilization each workload's response time is more sensitive to the share allocation: the lines in the figure are steeper. And at high utilization it is even clearer that share allocations affect workload 1 more than workload 2. That is because workload 1 has just half the utilization of workload 2, so when workload 1 has a small share there is lots of workload 2 processing that usually runs at higher priority. There is a moral to this story: if you give a heavy workload a large share (because its performance is important) you may seriously affect other lighter workloads. Conversely, giving a light workload a large share in order to improve its response time may not hurt the other workloads unacceptably much.
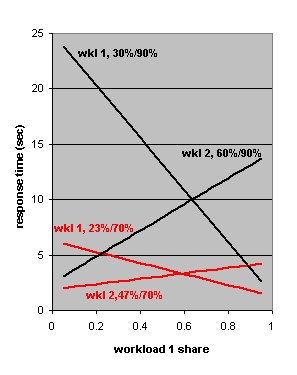
Figure 4. Response times for workloads 1 and 2 as a function of the share allocated workload 1 at total utilizations of 70% and 90%.
The lines representing the workload response times at a total utilization of 90% cross at a response time of 10 seconds, corresponding to a share allocation of 0.6+ for workload 1 and 0.3+ for workload 2. Those share allocations produce the response times that would be observed if no fair share scheduling were in effect: 1/(1 – 0.9) = 10 seconds for each workload. That's an easy consequence of the algebra in our model, and somewhat surprising: to make fair share scheduling for two workloads at high utilization mimic ordinary first come first served or round robin scheduling, allocate each workload a relative share that is the utilization of the other workload.
6. Comparing Models
In Figure 5 we compare the response time predictions of three models for fair share scheduling of two workloads. The first is the model presented in [Gun99] and [Sun99b]: a batch processing environment in which each workload runs a single process sequentially submitting one-second compute bound jobs (the formulae are in Section 2 above). The second two are transaction processing environments in which shares may be caps (Section 3.1) or guarantees (Section 3.2). In each of these cases workload utilizations are 30% and 60%.
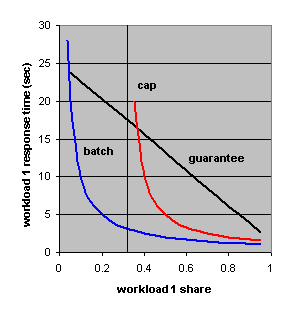
Figure 5. Response times for workload 1 as a function of its allocated share under three modeling assumptions: compute bound batch processing and transaction processing with share as caps and as guarantees.
The primary conclusion to draw from Figure 5 is that these models predict quite different behavior, so that it is important to choose the right one. The batch processing model yields results that are independent of workload utilizations. When shares are caps, shares must exceed utilizations. The figure shows that workload 1 response time increases without bound as its share decreases toward its utilization of 0.3. When shares are guarantees there is no unbounded behavior.
7. Many Transaction Workloads
Our discussion so far has focussed on the simple case in which there are just two workloads. Our model extends to handle more. When there are ![]() transaction workloads with guaranteed shares we again model the system by assuming that each of the
transaction workloads with guaranteed shares we again model the system by assuming that each of the ![]() possible priority orders occurs with a probability determined by the shares. Then we compute each workload’s response time as a weighted average of
possible priority orders occurs with a probability determined by the shares. Then we compute each workload’s response time as a weighted average of ![]() terms. Here is the average response time formula for workload 1 in the three workload case, with average service time normalized to 1. To emphasize the structure of the formula we have grouped the six terms according to the priority of workload 1:
terms. Here is the average response time formula for workload 1 in the three workload case, with average service time normalized to 1. To emphasize the structure of the formula we have grouped the six terms according to the priority of workload 1:
workload 1 response time
![]()
![]()
+ ![]()
+ ![]() ,
,
where ![]() is the probability that at any particular moment workload
is the probability that at any particular moment workload ![]() has the top priority, workload
has the top priority, workload ![]() the next and workload
the next and workload ![]() has the lowest priority. That probability is
has the lowest priority. That probability is
![]() ,
,
where ![]() ,
, ![]() , and
, and ![]() are the shares for workload
are the shares for workload ![]() ,
, ![]() , and
, and ![]() , respectively.
, respectively.
These formulae can be simplified algebraically. An optimizing compiler or a clever programmer would find many repeated sub-expressions to speed up the arithmetic. We have left them in this form so that you can see from the symmetry how they would generalize to more workloads.
When there are more than three workloads the formulae are too unwieldy to compute with by hand. We wrote a program to do the work. Visit http://www.bmc.com/patrol/fairshare.html to play with it. Even that program is not useful for large numbers of workloads since it runs in time O(n!). But you may not want to specify shares separately for many workloads, since the scheduling overhead increases with the complexity of the decisions the scheduler must make.
We tested our model by running a series of benchmarks on our IBM system. In each experiment the same random sequence of jobs was generated. The three workloads had utilizations 0.14, 0.21 and 0.39; we varied the CPU share assignments from (near) 0.0 to (near) 1.0 in increments of 0.2 in all possible ways that sum to 1.0: 21 experiments in all. Figure 6 shows how workload 1 response time varied as the share settings were changed: it is larger toward the rear of the picture where its share is smaller. The data for the other two workloads lead to similar pictures.
Figure 7 shows how our response time predictions compared with the measured values for workload 2 in each of the 21 experiments.
Figure 8 shows that the response time conservation predicted by the theory is confirmed by the experiments.
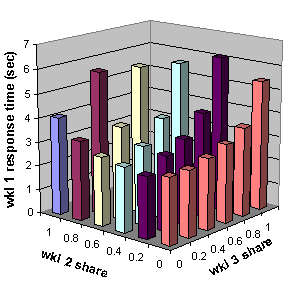
Figure 6. Workload 1 response time as a function of share settings when there are three workloads.
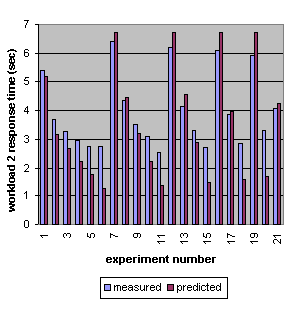
Figure 7. Workload 2 response time: measured vs. predicted values for each of the 21 experiments.
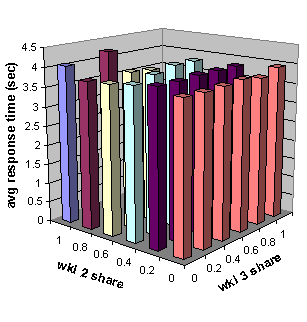
Figure 8. Weighted average response time as a function of share settings when there are three workloads.
8. Hierarchical Allocations
Fair share schedulers often allow for more sophisticated assignments of shares by arranging workloads as the leaves of a tree in which each node has a share. For example, suppose there are two production workloads that serve your customers’ computing needs and one development workload, and that you have assigned shares this way:
|
Group |
Share |
|
production customer 1 customer 2 |
0.8 0.4 0.6 |
|
development |
0.2 |
This scheme divides the 80% of the CPU allocated to production between the two customers in the ratio 4:6. Here too the analysis for compute bound work is straightforward. The shares multiply when you flatten the tree. Customer 1 will use 0.8
´ 0.4 = 32% of the CPU, customer 2 will use 48% and development 20%. The same fractions apply for transaction work if the shares are caps.But when the shares are guarantees the answer is different. We model the hierarchy by assuming that 80% of the time production work is at high priority and development work at low, and that whenever production is awarded the CPU, customer 1 is at high priority 40% of the time. So the system operates in one of four possible states with these probabilities:
|
Priority order |
Probability |
|
(c1, c2, dev) |
0.8 ´ 0.4 = 0.32 |
|
(c2, c1, dev) |
0.8 ´ 0.6 = 0.48 |
|
(dev, c1, c2) |
0.2 ´ 0.4 = 0.08 |
|
(dev, c2, c1) |
0.2 ´ 0.6 = 0.12 |
Then we compute the response times for each workload in each of the four states with standard formulas from queueing theory and use the probabilities to construct the weighted average response time for each workload. The answer will depend on the utilizations as well as the shares allocated to the workloads.
Once you accept the fact that flattening the tree is wrong for transaction workloads you can begin to understand why. Think about what happens when just workloads customer1 and development are competing for the processor. Because both customers are combined in a group, customer1 can use what’s guaranteed customer2. With the specified share hierarchy, customer1's work will progress four times as fast as development's. In the flattened tree it will progress only about one and a half times as fast (the ratio is 32/20). This illustrates a well known business phenomenon: customers can get a better deal by pooling their requests.
We conducted an SRM benchmark study that vividly illustrates this phenomenon. The following table shows the share allocation hierarchy, the measured utilizations and response times and the predicted response times for one second of CPU work.
|
Group |
Share |
Util |
Resp (meas) |
Resp (model) |
|
group-1-2 wkl 1 wkl 2 |
10000 10000 1 |
0.215 0.210 |
1.25 2.33 |
1.27 2.22 |
|
wkl 3 |
100 |
0.176 |
6.12 |
4.99 |
This hierarchy says essentially that group-1-2 always has priority over workload 3 (since the ratio of shares is 100:1) while within group-1-2 workload 1 has priority over workload 2. In the flattened configuration the ratio of the shares would be 10000:1:100, reversing the priority orders of workloads 2 and 3. Were that the case we would expect to see response times of 1.27, 5.23 and 2.09 for workloads 1, 2 and 3 respectively instead of the observed values that match the predictions from our model.
9. Summary
The ability to allocate resource shares to workloads is a powerful tool in the hands of administrators who need to guarantee predictable performance. To use such a tool wisely you should master a high level view before you start to tinker. Our model and the benchmark studies that validate it help you understand that
References
[BB83] Buzen, J. P., Bondi, A. R., "The Response Times of Priority Classes under Preemptive Resume in M/M/m Queues," Operations Research, Vol 31, No. 3, May-June, 1983
[Gun99] N. Gunther, Capacity Planning For Solaris SRM: "All I Ever Want is My Unfair Advantage" (And Why You Can’t Have It), Proc. CMG Conf., December 1999, pp194-205
[HP99] HP Process Resource Manager User’s Guide, Hewlett Packard, December 1999
[IBM00] AIX V4.3.3 Workload Manager Technical Reference, IBM, February 2000 Update
[Klein75] L. Kleinrock, "Queueing Systems Volume I: Theory," John Wiley & Sons, Inc. 1975
[KL88] J. Kay and P. Lauder, A Fair Share Scheduler, CACM, V31, No 1, January 1988, pp44-55
[Sun98] Solaris Resource Manager 1.0 White Paper, Sun Microsystems, 1998
[Sun99a] Solaris Resource Manager 1.1 Reference Manual, Sun Microsystems, August 1999
[Sun99b] Modelling the Behavior of Solaris Resource Manager, Sun BluePrints OnLine, August, 1999
http://www.sun.com/blueprints/0899/solaris4.pdf
[Wald95] Carl A. Waldspurger. Lottery and Stride Scheduling: Flexible Proportional-Share Resource Management, Ph.D. dissertation, Massachusetts Institute of Technology, September 1995. Also appears as Technical Report MIT/LCS/TR-667
http://www.waldspurger.org/carl/papers/phd-mit-tr667.ps.gz
[WW94] Carl A. Waldspurger and William E. Weihl. Lottery Scheduling: Flexible Proportional-Share Resource Management, Proceedings of the First Symposium on Operating Systems Design and Implementation (OSDI '94), pages 1-11, Monterey, California, November 1994
http://www/waldspurger.org/carl/papers/lottery-osdi94.ps.gz
Appendix 1. Experimental Configurations
|
Vendor/ Hardware |
OS |
Fair share scheduler |
|
HP 9000/839 Model K210 |
HP-UX 10.20 |
PRM C.01.07 |
|
IBM RS6000 7248 |
AIX 4.3.3 |
WLM |
|
Sun SPARCstation 20 Sun 4m |
Solaris 2.6 |
SRM |
Each machine was configured as a uniprocessor.
Appendix 2. Fair Share Scheduler Features
|
HP (HP-UX) PRM |
IBM (AIX) WLM |
Sun (Solaris) SRM |
|
|
Caps |
Yes |
Yes |
No |
|
Analysis |
Yes |
Yes |
Yes |
|
Setuid |
No |
No |
Yes |
|
Hierarchies |
No |
Yes |
Yes |
|
Group by Process |
Yes |
Yes |
No |
|
Group by User |
Yes |
Yes |
Yes |
Appendix 3: HP and IBM Two Workload Benchmark Results
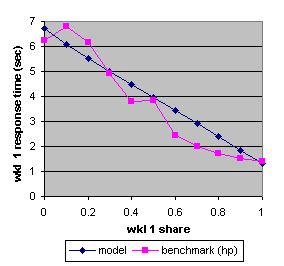
Figure 9. The benchmark and predicted average response times (HP) of workload 1 as a function of its allocated share.
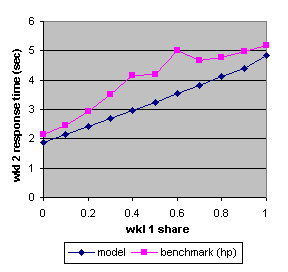
Figure 10. The benchmark and predicted average response times (HP) of workload 2 as a function of the share allocated to workload 1.
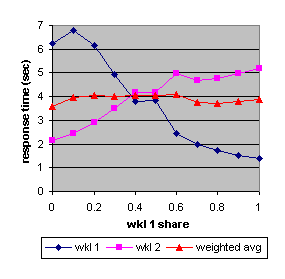
Figure 11. The measured response times (HP) of workload 1 and workload 2 as a function of the relative share allocated to workload 1 together with their average, weighted by their utilizations
.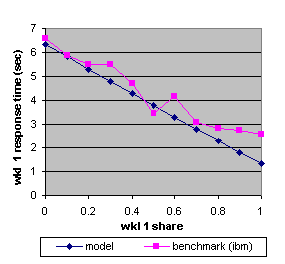
Figure 12. The benchmark and predicted average response times (IBM) of workload 1 as a function of its allocated share.
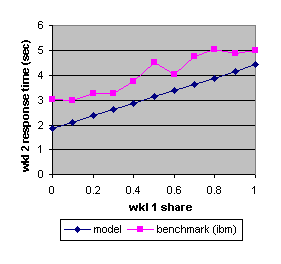
Figure 13. The benchmark and predicted average response times (IBM) of workload 2 as a function of the share allocated to workload 1.
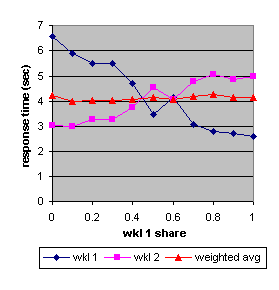
Figure 14. The measured response times (IBM) of workload 1 and workload 2 as a function of the relative share allocated to workload 1 together with their average, weighted by their utilizations.