The impetus to create this web page was the promise I made when my sliced cubes were accepted for the Mathematical Art Exhibit at the 2019 Joint Mathematics Meetings. Here's the gallery page.

I first saw this image when I was a high school freshman in 1950. It's from Hugo Steinhaus' Mathematical Snapshots.

In 1979 my friend Carl Steinitz arranged a visiting appointment for me at the Harvard Graduate School of Design, so I could play in their shop building models. One of the first things I did was bisect a cube. The halves in the back are from 4x4 pressure treated stock - you can see the ellipses. The halves in front are basswood. They fit together better because I took the kerf into account.

Staring at the basswood I imagined trisecting each half. That clearly couldn't be done by feeding it through the table saw - just the bisection was tricky. So I sketched the results, calculated the angles and cut the pieces from one inch hardwood scraps (from the trash bin at Anderson-McQuaid - they won't let you fish there any more).

The six slices that make one cube won't stand still together. So I made four cubes and a base to hold them.

I developed a reasonably efficient routine and made five sets of four cubes. I've given away three, to my grandson Solomon, to Tom Sallee, and to Paul Mason, years before he took the photos you see here.

This cube is sliced in sixths because each edge is bisected. I ventured further. If you cut one set of four parallel edges in thirds and bisect the other you slice the cube into seven pieces. I built a set of four such cubes, planing down the stock so that the assembled cube would be the same size as the six-sliced ones. That's a little tricky: the thickness of each slice isn't just 6/7 of what it was because the slicing planes are no longer perpendicular to the long diagonal.

When I was creating the wooden models folks said I should be using a computer. I resisted: hand sketches and hand calculations better matched the handiwork in the shop. Recently (i.e. 2016) I found myself with access to a 3D printer (in the maker space at the Heath elementary school in Brookline) so was tempted to try technology, which now does more than just the design. Here is that part of the story.

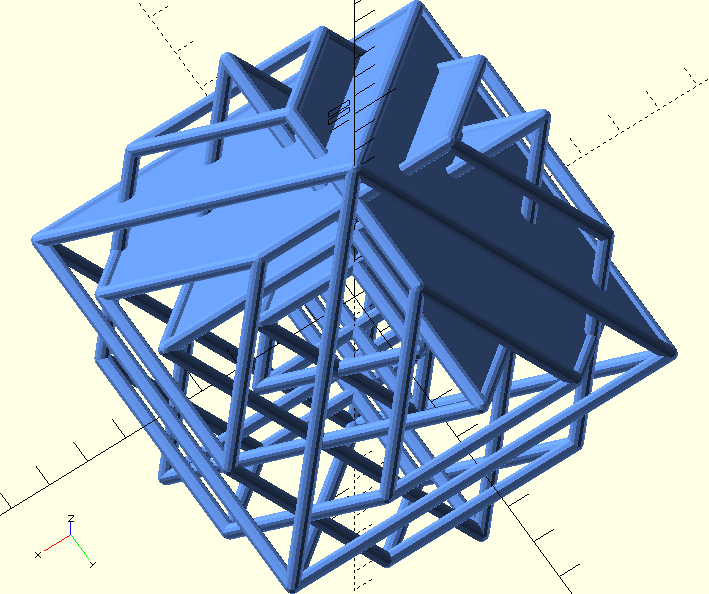
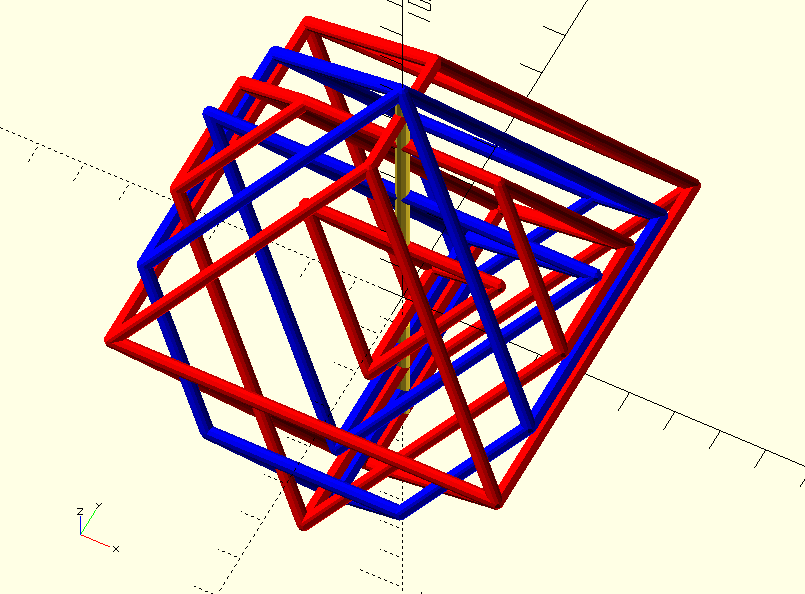
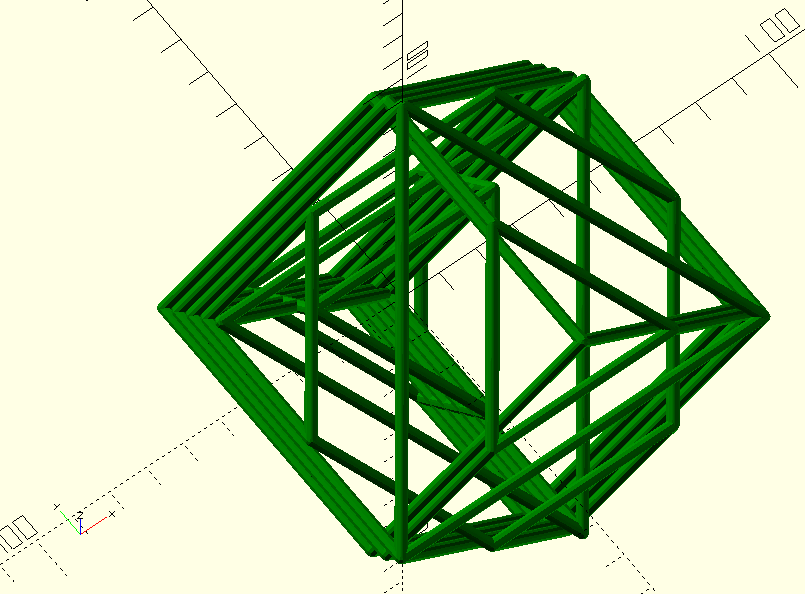
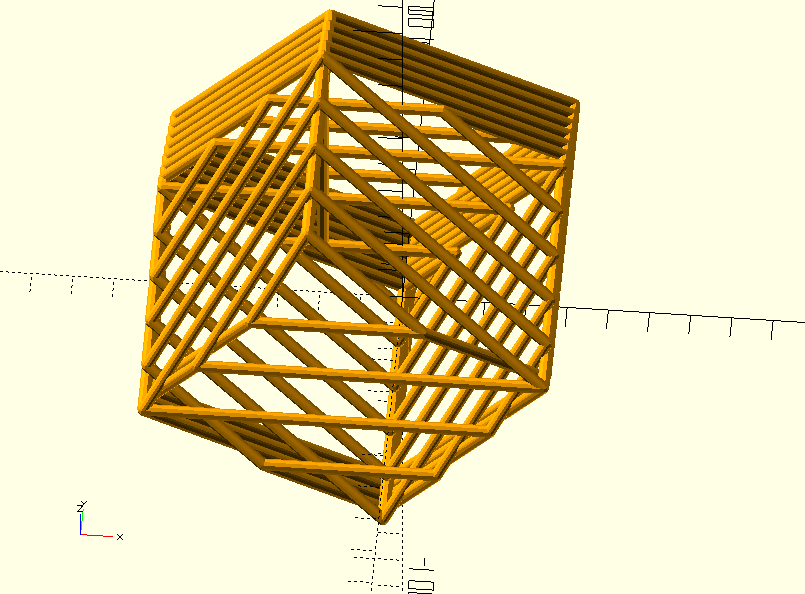
The 3D printing adventure continued in 2020 with projecting the skeletons of three dimensional slices of a tesseract. The openscad code is generated by a Python program that calculates the positions of the vertices. (Catalin Zara did the hard work.)

In these pictures the edges in the four directions are cut into (2,2,2,2), (2,2,3,3), (2,2,2,5) and (2,3,5,7) parts respectively.