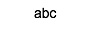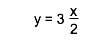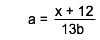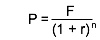IT 116: Introduction to Scripting

IT 116: Introduction to Scripting
Class 5

Microphone

Questions

Are there any questions before I begin?

Homework 3

I have posted homework 3 here.

It is due this coming Sunday at 11:59 PM.

Rules for Homework Scripts

You must follow certain rules when you create your homework scripts.

You will find those rules here.

Late Penalty

You will lose 2 points for every day that your assignment is late.

Every Unix file has a time stamp that changes every time the file is modified

My scripts at this time stamp to determine whether a submission is late.

If your assignment is not working by the due date ...

you can continue to work on it, but you will lose a few points.

If your assignment is working, do not go back and change it ...

because that will change the time stamp and result in a late penalty.

Do Not Email Me about Missing Assignments

If you get an email from me saying an assignment is missing do not email me about this.

I get far too many emails.

Instead of sending me an email, fix the problem.

If you do not know how to fix it, post a question on Piazza ...

or contact the Class Assistant.

I collect homework assignments and and check Class Exercises several times during the week.

I will check or collect your assignment later in the week.

Class Exercises

Scripts for each Class Exercise must have the correct filename ...

and be in the right directory ...

or my scripts will not see them.

If my scripts do not see them, your score with be zero.

If you receive no email from me about your Class Exercise script ...

that means your script will get full credit ...

less any late penalty that applies.

Course Work

Importance of Exams

Many people find exams difficult
But the best way for me to know if you have really learned the material is by giving exams
It is too easy to cheat on Class Exercises and homework assignments
This is why the two exams account for 50% of your grade
Too many students do well on the graded quizzes, Class Exercises and homework assignment ...
only to do poorly on the exams
This lowers their grade considerably
The purpose of the Class Exercises and homework assignments is to give you hands on experience with the material
And to better prepare you for the exams

Preparing for Exams

Both the midterm and final exams follow the same format
60% of the points on the exams come from questions taken from the ungraded class quizzes
The remaining 40% of the points come from 4 code questions
These questions ask you to write short segments of Python code
Two things will help you prepare for exams
- Flash cards
- Class Exercises and homework assignments
Flash cards should be made for all questions from Ungraded Class Quizzes
You should review them frequently throughout the semester
Pay attention when you are working on the Class Exercises and homeworks
Work on these assignments is teaching you how to write Python code
This will come in handy for answering the code questions on the midterm and final

Do Not Fall Behind in This Course

Technical courses require that you master a great deal of detail
You will need to study for this course several times during the week
Studying once a week is usually not enough
The key to success in a technical course is steady, consistant, work
It should be spread out over several days
Some important concepts do not sink in immediately
It may take several days for something new to become clear
Material in this course often depends on what came before
So it is critical that you not fall behind
If you fall behind, it can be VERY hard to catch up

Read the Homework Assignments Carefully

Homework assignments may ask you to do many things
So you may need to read the assignment more than once
A single reading might not be enough to understand what I want you to do
Take the time to read these documents slowly
This will help you understand all the details
If you don't, you will make mistakes and lose points
Technical work is detailed work
So you must learn to read documents with a lot of detail
If you do not understand something post a question on Piazza
NEVER GUESS at the meaning of something I have written

Tips and Examples

Representation of Data

Python has different data types for different kinds of values
Each data type has a different way of storing its value in memory
The string "5" appears in memory as the binary number 110101 ...
which is 53 in decimal ...
and is the number associated with the Unicode symbol "5"
The integer 5 appears as the binary number 101
The data type of a value determins what you can do it with
You can use an integer in arithmetic
But you can't do that with a string

Review

Expressions

Whenever we need a value in Python, we write an expression
An expression is anything that can be turned into a value
There are four different kinds of expressions
- Literals
- Variables
- Calculations involving operators
- Function calls
There are two places where expressions frequently occur
- Assignment statements
- As arguments in a function call
Whenever you need a value you can use any of the four kinds of expression
```
print("Hello")
print(rate)
print(rate * 1.1)
print(round(5.3))
```

Comments

When you write a program you understand its different parts
But will you remember what each part does a year from now ...
when you need to change it?
A program should be readable
That means that anyone who knows Python should be able to understand it
There are many ways to make a program readable
But one of the most important is to use comments
A comment is text written inside a script that is not read by the interpreter
In Python, any text on a line after a hash mark #...

is ignored by the interpreter

>>> print("Hello") # but ignore this text
Hello

If you want to write a multiline comment ...
each line must begin with a #

Variable Naming Rules

Variable names in Python must follow certain rules
- You cannot use words that have special meaning to Python as variable names
- Variable names cannot have spaces
- The first character of a variable name must be a letter, a-z and A-Z, or an underscore, _
- After the first character you can use letters, digits or the underscore
- Uppercase and lowercase letters are distinct
Words that have special meaning to Python are called keywords

Here is the list of Python keywords

False               def                 if                  raise
None                del                 import              return
True                elif                in                  try
and                 else                is                  while
as                  except              lambda              with
assert              finally             nonlocal            yield
break               for                 not                 
class               from                or                  
continue            global              pass

Python is case sensitive
That means that UPPERCASE letters and lowercase letters are completely different
This means that value and Value are the names of different variables

Choosing Good Variable Names

You should use variable names that make it clear what value the variable holds
So don't use d to hold the distance traveled
Use the variable name distance instead
Sometimes you need more than one word ...
to describe the value contained in a variable
When this happens, you should use the underscore character, _, to separate words
```
course_id
student_name
first_name
```

Numeric Data Types and Literals

A Python variable can hold many different types of values
- Strings
- Integers
- Decimals
Each of these types of values is stored in the computer's memory in a different binary pattern
The technical term for each of these different representations is a data type
When a string is stored in memory, its data type is str
When an integer is stored in memory, it has the data type int
When a decimal is stored, it has data type float
Float is short for floating point
Whenever we write a value directly into a Python statement ...
that value is called a literal
The data type of a value determines what you can do with it
You can add, subtract, multiply or divide integers and floats
But you cannot divide or subtract strings

Conversion Functions

Python has functions that convert from one data type to another
Use int() to convert a value into an integer
```
>>> int("5")
5
```
Use str() to convert a value into a string
```
>>> str(5)
'5'
```
Use float() to convert a value into a float
```
>>> float("5.35")
5.35
```

There are some values that cannot be converted

>>> int("five")
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: invalid literal for int() with base 10: 'five')
>>> int(7,500)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: int() base must be >= 2 and <= 36)

Reading Input from the Keyboard

A Python script can get a value from the user using the input function
input has one argument
That argument is text that will prompt the user for input
input is used in an assignment statement like this
```
VARIABLE_NAME = input(PROMPT)
```
When the interpreter gets to an assignment statement using input it
- Prints the prompt
- Waits for the user to enter text and hit Enter
- Stores the text entered at the command line into the variable

Here is an example

>>> team = input("Please enter a team name: ")
Please enter a team name: Red Sox
>>> print("Go", team)
Go Red Sox

The text in blue was entered by the user

Notice that I put a space at the end of the prompt string
It's good to have a gap between the prompt and the value entered by the user

Reading Numbers with the `input` Function

The value produced by the input function is always a string

This is true regardless of the value entered by the user

>>> number = input("Please enter a number: ")
Please enter a number: 55
>>> type(number)
<class 'str'>

If you want the value to be some other data type
You have to use a conversion function
To convert the variable number to an integer use the int function
```
>>>  number = int(number)
>>>  type(number)
<class 'int'>
```
You can ask for a number and covert it using two assignment statements
One to get input from the user with input ...
and another to convert the value into the right data type

You can also combine both operations into a single assignment statement

>>> number = int(input("Please enter an integer: "))
Please enter an integer: 67
>>> type(number)
<class 'int'>

Attendance

New Material

Performing Calculations

In Python's interactive mode, we can perform calculations
```
>>> 4 + 5
9
```
+ is an example of an operator
Operators are special characters that act upon one or more values ...
and perform an action
Usually that action produces a new value
The values that the operators work on are called operands

Python has operators for basic arithmetic

Character	Operation	Description
+	Addition	Adds two numbers
−	Subtraction	Subtracts one number from another
*	Multiplication	Multiplies one number by another
/	Division	Divides one number by another and gives the result as a decimal number
//	Integer division	Divides one number by another and gives the result as an integer
%	Remainder	Divides one number by another and gives the remainder
**	Exponent	Raises a number to a power

All these operators can be used with variables as well as numbers

>>> a = 2
>>> b = 4
>>> a + b
6
>>> a - b
-2
>>> a * b
8
>>> a / b
0.5

Decimal and Integer Division

Python has two division operators
- /
- //
The first works like ordinary division
```
>>> 4 / 2
2.0
>>> 4 / 5
0.8
```
Notice that the result is always a decimal
Even when the result is a whole number
This is decimal or floating-point division
// division always gives a whole number
When the result of the division is positive any fraction is thrown away
```
>>> 4 // 2
2
>>> 5 // 2
2
```
When the result of the division is negative the result is rounded down to the next lowest integer
```
>>> -4 // 2
-2
>>> -5 // 2
-3
```

Exponent Operator

** is the exponent operator
The number before this operator is raised to the power of the second number
```
>>> 3 ** 2
9
>>> 3 ** 3
27
>>> 3 ** 4
81
```

Remainder Operator

When we perform long division we get two results
- A quotient
- A remainder
If we divide 17 by 5 we get a quotient of 3
And a remainder of 2
Integer division, //, gives us the quotient
```
>>> 17 // 5
3
```
And we can get the remainder with %
```
>>> 17 % 5
2
```
The remainder operator is sometimes called the modulus operator
You can use the remainder operator to determine whether a number is odd or even
If, when we divide by 2, the remainder is 0, the number is even
If, when we divide by 2, the remainder is 1, the number is odd

Operator Precedence

We can use more than one operator in a calculation
```
>>> 2 + 3 + 5
10
```
When the operators are all the same, the order in which we do the operations does not matter
```
>>> 5 + 3 + 2
10
```
We could start at the left and work to the right
Or start at the right and work to the left
Order doesn't matter if we do addition and subtraction together
```
>>> 2 + 3 - 5
0
>>> -5 + 3 + 2
0
```
We get the same result if we first add 2 and 3 and then subtract 5
Or subtract 5 from 3 and then add 2
But with other combinations of operators the order does matter
What if the calculation was
```
2 + 3 * 5
```
Which operation do we do first?
Do we add 2 + 3 and then multiply by 5?
Or multiply 3 * 5 and add 2?
Running this calculation in Python gives
```
>>> 2 + 3 * 5
17
```
So Python does multiplication first
This is what you were taught in arithmetic class
That you do multiplication or division first
And then addition or subtraction
When I studied arithmetic we learned the phrase "My Dear Aunt Sally"
That stood for
M multiplication
D division
A addition
S subtraction
Whenever an expression has operators of different types ...
they must be applied in a specific order
This order is called operator precedence
The operator with the higher precedence is used first
Then the operator with the next highest precedence
And so on

The precedence for Python's arithmetic operators is

**	Exponentiation
* / // %	Multiplication, division and remainder
+ -	Addition and subtraction

Let's see how this works with the following calculation
```
4 + 3 * 5 ** 2
```
** has the highest precedence so first we raise 5 to the power of 2
```
5 ** 2 = 25
```
Then we multiply this result by 3
```
3 * 25 = 75
```
Then we add 4
```
4 + 75 = 79
```
This is indeed the value that Python gives us
```
>>> 4 + 3 * 5 ** 2
79
```

Grouping with Parentheses

But what if we wanted to evalaute the operators in the order in which they were written?
What if we wanted to first add 4 and 3
Then multiply the result by 5
Then square that result?
We can use operators in an order different from the order of precedence
We do this using parentheses, ( )
To first add 2 + 3 then multiply by 5 we write
```
(4 + 3) * 5 = 35
```
Parentheses are not operators
But they override the normal order of precedence
Calculations inside parentheses must be done first ...
before using operators outside the parentheses
I'm told that nowadays arithmetic teachers no longer use "My Dear Aunt Sally"
Instead they tell their student to remember PEMDAS
P - Parentheses
E - Exponent (raising to a power)
M - Multiplication
D - Division
A - Addition
S - Subtractions
This mnemonic (memory aid) is useful because it includes exponentiation
But parentheses are not operators ...
because they perform no action

Mixed-Type Expressions and Data Type Conversion

If you multiply two integers, you get an integer
```
>>> 3 * 5
15
```
If you multiply two decimals, you get a decimal
```
>>> 3.0 * 5.0
15.0
```
But what if you multiply an integer by a decimal?
In Python, you will get a decimal
```
>>> 3 * 5.0
15.0
```
Here are the rules
- When an operation is performed on two int values, the result will be an int
- When an operation is performed on two float values, the result will be a float
- When an operation is performed on an int and a float, the result of the operation will be a float
An expression that uses operands of different data types is called a mixed-type expression
If you need to convert a value into an integer you can use the int conversion function
You can use int with strings as long as the characters are only digits
```
>>> int("534")
534
```

But don't put a decimal point inside the string

>>> int("5.6")
Traceback (most recent call last):
  File <stdin>, line 1, in <module>
ValueError: invalid literal for int() with base 10: '5.6'

If you run int on a decimal value it will throw away the digits after the decimal point
```
>>> int(5.78)
5
```
In other words, it does not round
There is a round function for that
```
>>> round(5.78)
6
```
If you need to convert a value into a float you can use the float() conversion function
It will work with strings that contain digits and one decimal point
```
>>> float("5.78")
5.78
```

But not two decimal points

>>> float("5.7.8")
Traceback (most recent call last):
  File <stdin>, line 1, in <module>
ValueError: could not convert string to float: '5.7.8'

float will also work with integers
```
>>> float(5)
5.0
```

Breaking Long Statements into Multiple Lines

Statements are the basic unit of Python programs
In some languages, like C and Java ...
you have to mark the end of each statement with a semi-colon, ;
This makes it easy to write long lines of code
You can continue a statement onto as many lines as you want ...
and just put ; at the end
But most statements are short
Having to put a ; at the end of every statement is very annoying
It means extra typing
And if you forget the semicolon you get an error
So Python does not do this
A statement can be as long as you like
And there is no need to put a special character at the end of the line
This is makes life easy as long as your statements are short
But sometimes you have to write a long statement
Python does not care how long the statement is
As long as it is on a single line
In most editors this just means that the line continues ...
to the edge of the window ...
and then continues on the next line
But the break will usually occur in the middle of a word ...
which would make it hard to read
It's best to have all you statements fit inside your window
That way you can read your code without changing the width of the window
You can break a long Python statement into two or more lines

You do this by hitting backslash, \ , before hitting Enter

>>> print("To be or not to be. \
... That is the question.")
To be or not to be. That is the question.

Expressions inside Expressions

In the last class I showed you two statements

number = input("Please enter a number: ")
number = int(number)

I told you they could be written as a single statement
```
number = int(input("Please enter an integer: "))
```
This is legal Python because a function call can take any expression as its argument
A function call that returns a value is itself an expression
So the argument to a function call can be another function call
In the statement above the argument to int is a function call to input

Converting Algebra Into Python

You may have noticed that when we write the Python expression
```
a + b 
```
it looks like something you saw in algebra
But there are important difference between Python and algebra
In algebra variable names are always a single letter
It is legal to have a Python variable whose name is a single letter
But it is not good practice
Variable names should say something about the value they hold
There are other differences
In algebra when we write

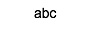
We mean that the value of a is multiplied by the value of b ...
and that result is in turn is multiplied by the value of c
In Python we would write this as
```
a * b * c
```
Similarly, the algebraic expression

would be written like this in Python
```
12 * 4
```
The following algebraic formula

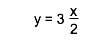
Would look like this in Python
```
y = 3 * x / 2
```
Similarly the formula

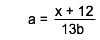
in Python would be
```
a = (x + 12) / (13 * b)
```
Notice that we had to put both the numerator
```
x + 12
```
and the denominator
```
13 * b
```
inside parentheses
We have to calculate the value of each of these expressions before dividing them
This is were the rules of precedence swing into action
The financial formula

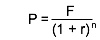
Would become the following in Python
```
P = F / (1 + r) ** n
```

Course Work

Tips and Examples

Review

New Material

Questions

Homework 3

Rules for Homework Scripts

Late Penalty

Do Not Email Me about Missing Assignments

Class Exercises

Course Work

Importance of Exams

Preparing for Exams

Do Not Fall Behind in This Course

Read the Homework Assignments Carefully

Tips and Examples

Representation of Data

Review

Expressions

Comments

Variable Naming Rules

Choosing Good Variable Names

Numeric Data Types and Literals

Conversion Functions

Reading Input from the Keyboard

Reading Numbers with the input Function

Attendance

New Material

Performing Calculations

Decimal and Integer Division

Exponent Operator

Remainder Operator

Operator Precedence

Grouping with Parentheses

Mixed-Type Expressions and Data Type Conversion

Breaking Long Statements into Multiple Lines

Expressions inside Expressions

Converting Algebra Into Python

Class Exercise

Class Quiz

Reading Numbers with the `input` Function