for Loops with Setsmin And max with SetsAre there any questions before I begin?
You can connect to Gradescope to take weekly graded quiz today during the last 15 minutes of the class.
Once you start the quiz you have 15 minutes to finish it.
You can only take this quiz today.
There is no makeup for the weekly quiz.
I have posted a solution to homework 3 here.
Let's take a look.
I have posted homework 5 here.
It is due this coming Sunday at 11:59 PM.
if statements and while loops need boolean valuesWiliam Campbell (Bill)
if statement
if preferred:
preferred = "(" + preferred + ")"
if len(preferred) > 0:
preferred = "(" + preferred + ")"
x ∈ A
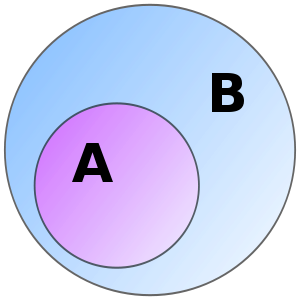
A ⊂ B
B ⊃ A
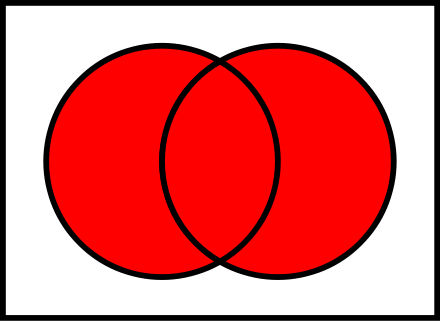
A ∪ B
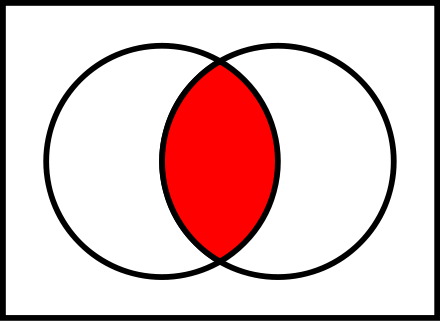
A ∩ B
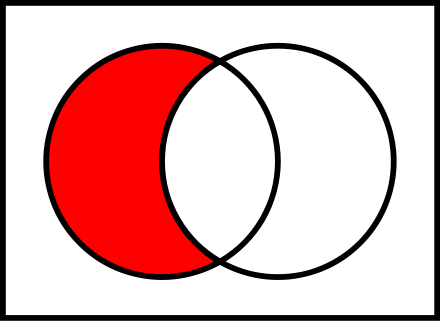
A - B
A Δ B
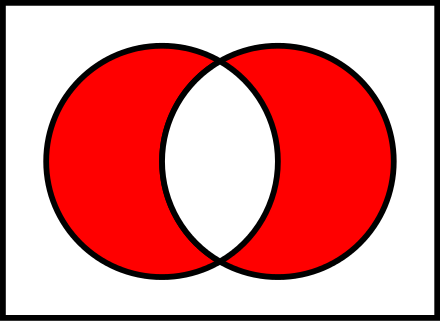
set functionset takes a single argument for loopset
>>> num_list = [1,2,3]
>>> num_set = set(num_list)
>>> num_set
{1, 2, 3}
>>> list_1 = [1, 2, 3, 4, 5] >>> type(list_1) <class 'list'>
>>> nonsense = {'foo', 'bar', 'bletch'}
>>> type(nonsense)
<class 'set'>
>>> empty = [] >>> type(empty) <class 'list'>
>>> empty = {}
>>> type(empty)
<class 'dict'>
set with no arguments
>>> set_1 = set() >>> set_1 set()
>>> set_2 = {}
>>> type(set_2) <class 'dict'>
empty_set = set()
>>> empty_set set()
>>> s1 = set() >>> s1 set()
>>> s1.add(1)
>>> s1
{1}
>>> s1.add('two')
>>> s1
{1, 'two'}
>>> s1.add((3,3,3))
>>> s1
{(3, 3, 3), 1, 'two'}
>>> s1.add(1)
>>> s1
{(3, 3, 3), 1, 'two'}
>>> s2 = set()
>>> s2
set()
>>> s2.update([1, 2, 3])
>>> s2
{1, 2, 3}
>>> s2.update('foo')
>>> s2
{1, 2, 3, 'f', 'o'}
>>> numb_set
{1, 2, 3, 4, 5}
>>> numb_set.discard(2)
>>> numb_set
{1, 3, 4, 5}
>>> numb_set.remove(4)
>>> numb_set
{1, 3, 5}
>>> numb_set.discard(2)
>>> numb_set
{1, 3, 5}
>>> numb_set.remove(4)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
KeyError: 4
len function gives the size of a set
>>> s1 = {1, 2, 3}
>>> len(s1)
3
>>> s2 = {3, 2, 1}
>>> len(s2)
3
>>> s3 = {'one', 'two', 'three', 'four'}
>>> len(s3)
4
len function on each to get their size>>> list_1 = [1, 2, 3] >>> list_2 = [3, 2, 1] >>> list_1 == list_2 False
>>> s1 = {1, 2, 3}
>>> s2 = {3, 2, 1}
>>> s1 == s2
True
>>> tuple_set = {(1,2), (3,4), (5,6)}
>>> tuple_set
{(5, 6), (1, 2), (3, 4)}
>>> list_set = {[1,2], [3,4], [5,6]}
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'list'
>>> a, b, c = 1, 2, 3
>>> A = {a, b, c}
>>> A
{1, 2, 3}
>>> a = 5
>>> A
{1, 2, 3}
for Loops with Setsfor loopfor loop looks like this
for LOOP_VARIABLE in ITERABLE_OBJECT:
STATEMENT
...
>>> s1 = {1, 2, 3, 4, 5}
>>> for number in s1:
... print(number)
...
1
2
3
4
5
>>> s2 = {'one', 'two', 'three', 'four', 'five'}
>>> for number in s2:
... print(number)
...
two
five
three
one
four
>>> list_1 = [1, 2, 3, 4, 5] >>> for number in list_1: ... print(number) ... 1 2 3 4 5 >>> list_2 = [5, 4, 3, 2, 1] >>> for number in list_2: ... print(number) ... 5 4 3 2 1
in
operator
>>> list_1 [5, 4, 3, 2, 1] >>> 7 in list_1 False >>> 5 in list_1 True
in operator ...
>>> s1
{1, 2, 3, 4, 5}
>>> 7 in s1
False
>>> 8 in s1
False
>>> 3 in s1
True
not in operator
>>> 8 not in s1 True >>> 3 not in s1 False
not in are two words ...A ∪ B
>>> A = {1, 4, 8, 12}
>>> B = {1, 2, 6, 8}
>>> A.union(B)
{1, 2, 4, 6, 8, 12}
A ∪ B
B ∪ A
>>> B.union(A)
{1, 2, 4, 6, 8, 12}
>>> A | B
{1, 2, 4, 6, 8, 12}
>>> B | A
{1, 2, 4, 6, 8, 12}
A ∩ B
>>> A
{8, 1, 12, 4}
>>> B
{8, 1, 2, 6}
>>> A.intersection(B)
{8, 1}
A ∩ B = B ∩ A
>>> B.intersection(A)
{8, 1}
>>> A & B
{8, 1}
>>> B & A
{8, 1}
A & B == B & A
True
A that are
not in B
A - B
>>> A
{8, 1, 12, 4}
>>> B
{8, 1, 2, 6}
A.difference(B)
{12, 4}
A - B ≠ B - A
>>> B.difference(A)
{2, 6}
>>> A - B
{12, 4}
>>> A - B == B - A False >>> A - B != B - A True
A Δ B
>>> A
{8, 1, 12, 4}
>>> B
{8, 1, 2, 6}
>>> A.symmetric_difference(B)
{2, 4, 6, 12}
A Δ B = B Δ A
B.symmetric_difference(A)
{2, 4, 6, 12}
A ^ B
{2, 4, 6, 12}
>>> A ^ B == B ^ A True
| Operator | Operation |
|---|---|
| | | union |
| & | intersection |
| - | difference |
| ^ | symmetric difference |
>>> s1 = {1,3,5}
>>> s2 = {2,4,6}
>>> s1 | s2
{1, 2, 3, 4, 5, 6}
>>> n1 = 3 >>> n2 = 5 >>> n1 += n2 >>> n1 8
s1 = s1 | s2
>>> s1 |= s2
>>> s1
{1, 2, 3, 4, 5, 6}
>>> A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
>>> B = {1, 3, 5, 7, 9}
>>> A.issubset(B) False >>> B.issubset(A) True
>>> A <= B False >>> B <= A True
>>> A.issuperset(B) True >>> B.issuperset(A) False
>>> A >= B True >>> B >= A False
>>> odds = {1, 3, 5, 7, 9}
>>> evens = {2, 4, 6, 8, 10}
>>> evens.isdisjoint(odds)
True
>>> odds.isdisjoint(even) True
>>> D = {1, 2, 3, 4, 5}
>>> D
{1, 2, 3, 4, 5}
>>> D.clear()
>>> D
set()
min And max with Setsmax built-in function
>>> B = {1, 3, 5, 7, 9}
>>> max(B)
9
min function
>>> min(B) 1
>>> s1 ={1, "q", 5, "kk", 87}
>>> max(s1)
Traceback (most recent call last):
File "<;stdin>;", line 1, in <module>
TypeError: '>' not supported between instances of 'str' and 'int'
>>> min(s1)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: '<' not supported between instances of 'str' and 'int'
emails_1 = []
emails_2 = []
for line in email_file_1:
emails_1.append(line.strip())
for line in email_file_2:
emails_2.append(line.strip())
emails_new = emails_1[:]
for email in emails_2:
if email not in emails_new:
emails_new.append(email)
$ ./merge_emails_1.py Email file 1: emails_1.txt Email file 2: emails_2.txt List 1 Glenn.Hoffman@umb.edu big_bill@hotmail.com larry.wall@gmail.com timsmith@yahoo.com bigorangeshithead@whitehouse.gov List 2 Glenn.Hoffman@umb.edu alanh@hotmail.com timsmith@yahoo.com davidm@mac.com billybob@cs.umb.edu Merged list Glenn.Hoffman@umb.edu big_bill@hotmail.com larry.wall@gmail.com timsmith@yahoo.com bigorangeshithead@whitehouse.gov alanh@hotmail.com davidm@mac.com billybob@cs.umb.edu
emails_new = emails_1.union(emails_2)
>>> it244 = {"01459659", "00709552", "01565798", "00974687", "01357397", "01107434",
... "01516157", "01470962", "01015502", "01283749", "01313387", "01113342",
... "01684609", "01018750", "01458680", "01530289", "01600144"}
>>> it116 = {"01276750", "01246473", "01146053", "01361550", "01330451", "01405338",
... "01240592", "01328324", "01393077", "00822499", "01158165", "01342910",
... "01559794", "01293714", "01352486", "01367216", "01165111", "01617531",
... "01485027", "01397047", "01459659"}
>>> a = 01684609
File "<stdin>", line 1
a = 01684609
^
SyntaxError: invalid token
>>> it244.intersection(it116)
{'01459659'}
>>> all_students = it244 | it116
>>> len(it244) 17 >>> len(it116) 21 >>> len(all_students) 37
>>> athletes = basketball | baseball
>>>report_needed = all_students & athletes
>>> report_needed
{'01146053', '01015502', '01367216', '01330451'}
create a tuple of first names
create a tuple of last names
ask the user for the number of names required
create an empty set full_names
while the length of full_names is less than number required:
create a full name from a randomly chosen first name and last name
add this full name to full_names
for each name in full_names:
print the name