LIMITS

Return to Contents

1.  Enter the limit and sketch a graph. Show all  asymptotes.


lim
x ® 4 
 x-4
2x+3

2.  Find the limit. Enter the numerator first followed by the denominator:


lim
x ® a 
 x-4
2x+3

3. Find and enter the limit. Sketch the graph paying attention to any asymptotes.


lim
x ® -3 
 x2-x-12
x+3

4. Prove that


lim
x ® 3 
 (4x-5) = 7     by finding a rule     d = d(e)

Enter the numerator of the rule followed by the denominator (use e for epsilon):

5. Find the following limit:


lim
h ® 0 
 (3+h)2 - 9
h
6. Enter the following limit:

lim
x ® 0+ 
 |x|
x
7. Sketch the graph of the Greatest Integer Function. Enter the limit:

lim
x ® 1+ 
 [[x]]

8.

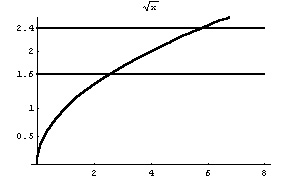
Use the given graph to find  the largest   d > 0    such that     |   __
Ö x
 
 - 2 | < 0.4     if     0 < |x - 4| < d
Enter d    to 2 decimal places

9. Find the limit.


lim
t ® 0 
 Sin(5t)
t

10. Find the limit and enter below:(numerator followed by denominator)

lim
x ® 0 
 tan(x)
3x
 

11. Sketch the graph. Enter the limit. Support your answer by an argument.

 


lim
x ® 0 
 x2 Sin æ
ç
è 		1
x
 ö
÷
ø

12. Find the following limit:

lim
x ® ±¥ 
 2x3 + 3x
x3 +1

Return to Contents