Homework 13🔗

Last updated: Tue, 6 May 2025 09:14:51 -0400

Out: Tue May 06 2025, 11am EST

Due: Tue May 13 2025, 11am EST

Overview🔗

In this assignment, you will get to use the "450lang" "high-level language" that you created!

This hw will be graded accordingly:

Setup🔗

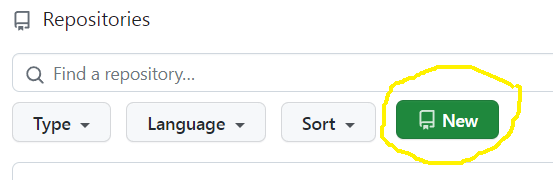
Create a new repository for this assignment by going to the CS450 Spring 2025 GitHub Organization and clicking "New".

Note: The CS450 Spring 2025 GitHub Organization must be the owner of the repository. Do not create the repository in your own account.

On the "Create a new repository" screen:

• Name the repository hw<X>-<LASTNAME>-<FIRSTNAME> where <X> is the current homework number.

  For example, I would name my hw13 repository hw13-Chang-Stephen.

• Mark the repository as Private.

• Check "Add a README file".

• Select the Racket template for the .gitignore.

• Choose whatever you wish for the license.

When done click "Create repository".

NEW!

Installing 450Lang

In this assignment, we will use our "450 lang" programming language, so we must install it first.

The easiest way to do so is from DrRacket, go to File -> Package Manager, and then install the 450lang package. This will allow you to use the language by writing #lang 450lang at the top of a file.

(If you installed it before this hw, make sure to update the package, also via DrRacket Pacakge Manager, to get the latest changes.)

Tasks🔗

Reading

• (Re)read Chapters 25-30 Textbook.

• Review the The Design Recipe section of the course website, particularly the sections on accumulators and generative recursion.

Pre-programming Notes

• All code must be written using #lang 450lang. Here is a specification for the programming language.

• All code must still be written following the The Design Recipe. (Just submitting code is not sufficient.)

• For Examples and Tests, use the 450lang built-in testing forms (see the testing part of the language specification).

  Examples and Tests for a function definition should be right after the definition. Try to think about corner cases and code coverage to achieve "sufficient" Tests.

• The submitted program must be only a series of definitions and tests. It should not run any other code. Not following this will result in GradeScope errors and/or timeouts.

• So long as you cite it properly, you may use any sources (including AI companion tools) to help you clarify or understand the problem. These are all well-known problems so you should have no problems finding information about them.

• Important: Each submission must be organized so that each function only processes one kind of data. Submissions consisting of only a few large, unreadable functions that try to do everything will not receive any credit.

Programming

In this assignment, you must use the "450lang" programming language. See the specification for the programming language. In addition to the features from previous assignments, there are additional features that have been added such as lists and other primitives.

Specifically, you must solve a version of the "n-queens" puzzle, similar to the one described in Chapter 29.2 of the textbook, by writing the following recursive functions. Make sure to follow the Design Recipe, especially for Accumulators and Generative Recursion when needed.

Data Definitions

• Qx and Qy are integers in the range [1,n], where "n" depends on the variant of the "n-queens" problem being solved. Represents a row/column on an n by n chessboard (ascending left-to-right and top-to-bottom).

• A Queen is a (Q Qx Qy), where Q is a constructor you must define. Represents a row and column position of a queen (on an n by n chess board). You should also define accessors named qx and qy that extract the row and column, respectively.

Functions

Before Submitting🔗

Testing (and Autograders)

Before submitting, note:

• Do not submit until all code has been thoroughly tested (by you), which means writing a "sufficient" number of Test cases.

• A GradeScope "Autograder" may or may not be released before the due date but either way, an Autograder is not a software development/testing tool, so do not use it as one. Code must be tested independent of any Autograder and questions about Autograders will be ignored (e.g., posts asking "why is the Autograder giving an error?" are not allowed)

• If you do submit before the deadline and get an Autograder error, this is bonus information that indicates the submitted code is not complete and/or not correct. But it’s up to you to figure out what "correct" means and how to fix to the program.

• Of course, the course staff is here and eager to help, but cannot do so without context information. The best way to supply this information is to INCLUDE EXAMPLES WITH ALL QUESTIONS, along with what the "expected" result should be! The posted examples should be the minimal amount of code needed to communicate the problem. This will receive the clearest possible answer.

• The Autograder test suite is subject to change. This means that the visible grade seen during submission is not the final grade.

Style

All code should follow proper Racket Style.

Also, the repository itself must follow proper style. Specifically, it must have appropriate commit messages. See How to Write a Git Commit Message if you are unsure how to write a commit message.

Files

A submission must have the following files in the repository root:

• hw13.rkt: Contains the hw solution code.

  Code must be written with (i.e., the first line should be) #lang racket.

  All definitions should use the name specified in the exercise (ask if you are unsure).

• README.md: Contains the required README information, including the GitHub repo url.

Submitting🔗

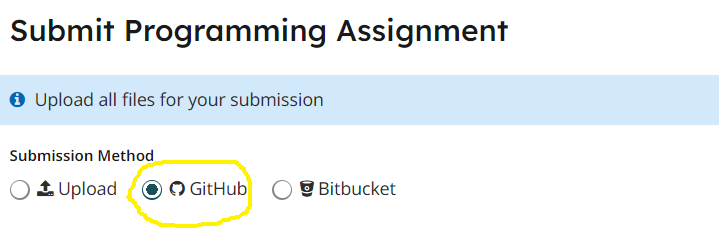
When you are done, submit your work to Gradescope hw13. You must use the "GitHub" Submission Method and select your hw<X>-<LASTNAME>-<FIRSTNAME> repository.

Note that this is the only acceptable way to submit homework in this course. (Do not manually upload files and do not email files to the course staff. Homework submitted via any unapproved methods will not be graded.)