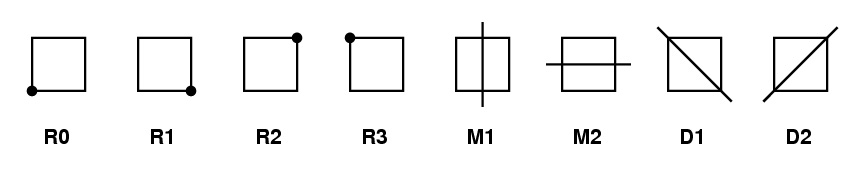
The square has eight symmetries - four rotations, two mirror images, and two diagonal flips:

These eight form a group under composition (do one, then another). Let's give each one a color:

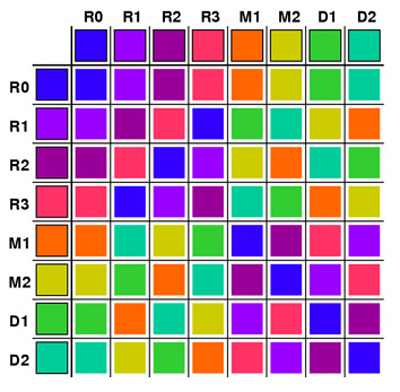 |
You can rotate the square in the eight possible ways by clicking on successive buttons to see which element results. Note: this group is not abelian, clicking is not commutative. To use the multiplication table the first operation is the column index and the second the row. Thus R1 followed by M1 is D2, while M1 followed by R1 is D1.
Warning. When using Internet Explorer sometimes the first click after loading the applet does nothing. Behavior is fine with firefox.
The colorful design and original applet code is the work of Erin Carmody at the MSRI Mathematical Graphics Workshop for undergraduate math majors held at Reed College in 2005. Visit her at www.erincarmody.org/. You can see her version of the applet at merganser.math.gvsu.edu/david/reed05/projects/carmody/html/presentation.html. Ethan Bolker rewrote the applet in June 2007 for Yu Zhang to use in her thesis. The source code for this version is in file RotateSquare.java. To run the applet as an application, or to modify it, you will need the jar file rotate.jar.
I think it would make an interesting exercise to generalize this application so that it calculated in an arbitrary dihedral group. Some students at the Reed summer institute started the job two years earlier, but without Carmody's sense of color. You can see their work at http://merganser.math.gvsu.edu/david/reed03/projects/ettingerGuy/.