Homework 8🔗

Last updated: Fri, 31 Oct 2025 13:20:58 -0400

Out: Mon Oct 27, 12:00pm EDT (noon) Due: Mon Nov 03, 12:00pm EDT (noon)

Note: Assignments are not officially "released" until—and are subject to change without notice up to—the indicated "Out" date and time. If an assignment is posted early, students may look ahead but are responsible for ensuring that they are always working with the most recent version of the homework.

This assignment continues looking at context-free languages, and begins to explore Turing Machines

Homework Problems

1. CFLs and Star (16 points)

2. Are Regular Languages CFLs? (16 points)

3. How a Turing Machine Computes (16 points)

4. README (2 point)

Total: 50 points

Submitting

Submit your solution to this assignment in Gradescope hw8. Please assign each page to the correct problem and make sure your solutions are legible.

A submission must also include a README containing the required information.

1 CFLs and Star🔗

Prove that the set of context-free languages are closed under the Kleene Star operation.

Use the definition of the "Star" function on languages from lecture (or Sipser 1.23).

Your proof may only use PDAs. This means that your proof should define a function \mathrm{STAR}_\textsf{PDA} : \textsf{PDA} \rightarrow \textsf{PDA} such that for any PDA P, L(\textrm{STAR}_\textsf{PDA}(P))=L(P)^*. You should not, however, explicitly prove the correctness the \textrm{STAR}_\textsf{PDA} function. Instead you should use an Examples Table in the proof.

A correct solution must include the following components:

1. An explicitly stated IF-THEN Statement to Prove (please ask if there is any confusion here, if this part is not correct, then the rest of the problem will also not be correct)

2. A proof of the exact statement above in the usual Statements / Justifications Table. Any solutions that prove a different theorem or answer a different question will not receive credit.

3. A definition of \mathrm{STAR}_\textsf{PDA} separate from, but referenced from, the main proof table

4. If the proof has a statement of the form "SOME-MACHINE recognizes SOME-LANGUAGE" (which it should), this must be justified with an Examples Table, separate from the main proof table, that demonstrates the is machine correct with respect to the language. The table should include both examples in the language and not in the language, should cover all paths through the machine, and should think about corner cases. Also, if the proof does not involve one specific machine or language, then the Examples Table needs Justifications.

2 Are Regular Languages CFLs?🔗

Prove that every regular language is a CFL.

Your proof may only use NFAs and PDAs. This means that your proof should define a function \mathrm{CONVERT}_\textsf{NFA-PDA} : \textsf{NFA} \rightarrow \textsf{PDA} such that for any NFA N, L(\textrm{CONVERT}_\textsf{NFA-PDA}(N))=L(N). You should not, however, explicitly prove the correctness of the \mathrm{CONVERT}_\textsf{NFA-PDA} function. Instead you should use an Examples Table in the proof.

A correct solution must include the following components:

1. An explicitly stated IF-THEN Statement to Prove (please ask if there is any confusion here, if this part is not correct, then the rest of the problem will also not be correct)

2. A proof of the exact statement above in the usual Statements / Justifications Table. Any solutions that prove a different theorem or answer a different question will not receive credit.

3. A definition of \mathrm{CONVERT}_\textsf{NFA-PDA} separate from the main proof table

4. If the proof has a statement of the form "SOME-MACHINE recognizes SOME-LANGUAGE" (which it should), this must be justified with an Examples Table, separate from the main proof table, that demonstrates the is machine correct with respect to the language. The table should include both examples in the language and not in the language, should cover all paths through the machine, and should think about corner cases. Also, if the proof does not involve one specific machine or language, then the Examples Table needs Justifications.

3 How a Turing Machine Computes🔗

Here is a Turing Machine state diagram from class (Figure 3.10 in the Sipser Textbook):

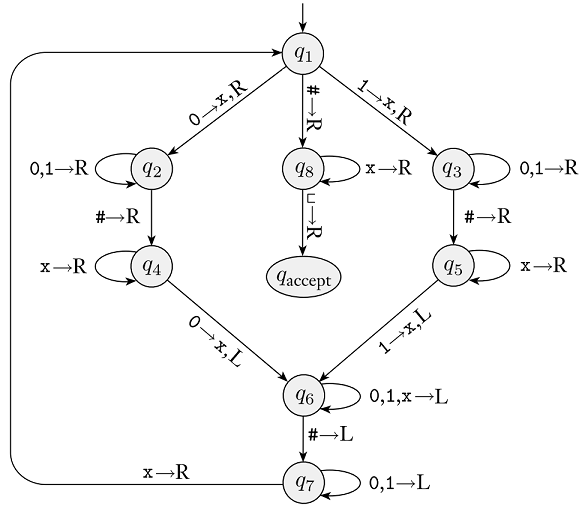
Remember that from each state, there are implicit transitions to an implicit q_{reject} state for any alphabet characters that are not explicitly shown. You may assume that transitions that go to q_{reject} do not change the tape contents and move the head to the right. Also, if a transition does not have a "write" character, then the tape contents stay the same (i.e., it "writes" the same character that was there).

Using this machine, answer the following questions (if your answer includes TM configurations, they must be the textual representation of a configuration).

1. What is the start configuration of this machine for an input string with characters \texttt{11111101001}?

2. Give two concrete strings accepted by this TM. Then, for each of these strings, give a sequence of configurations that starts in the start configuration and ends in a configuration containing q_{accept}. The two sequences of configurations that you submit must together use every (shown) transition in the machine. Make sure that the head is pointing at the correct character at each step.

3. Give two concrete strings rejected by this TM. Then, for each of these strings, give a sequence of configurations that starts in the start configuration and ends in a configuration containing q_{reject}.

4. When a Turing Machine is given an input string and begins computation on that string, what are the possible results of the computation?

5. For strings that should be in the language of a Turing Machine, what are the possible results of the computation? For strings that are not in the language of a Turing Machine, what are the possible results of the computation?