Homework 3
Last updated: Sat, 27 Sep 2025 19:06:30 -0400
Out: Mon Sept 22, 12:00pm EDT (noon) Due: Mon Sept 29, 12:00pm EDT (noon)
Note: Assignments are not officially "released" until—
and are subject to change without notice up to— the indicated "Out" date and time. If an assignment is posted early, students may look ahead but are responsible for ensuring that they are always working with the most recent version of the homework.
This assignment explores the concept of closed operations on regular languages.
Homework Problems
A Function on Languages (12 points)
Are Regular Languages Closed Under \mathrm{MAKECS}? (12 points)
DFAs vs NFAs (12 points)
README (1 point)
Total: 37 points
Submitting
Submit your solution to this assignment in Gradescope hw3. Please assign each page to the correct problem and make sure your solutions are legible.
A submission must also include a README containing the required information.
1 A Function on Languages
Consider a function, called \mathrm{MAKECS}, which converts an input language to a new output language such that for each string w in the input language, there is a corresponding string in the output language that starts with the characters cs and ends in the characters of w.
Formally:
\mathrm{MAKECS}(L)=\{\texttt{cs}w\mid \textrm{ where }w\textrm{ is a string}\in L\}
If the alphabet for a language L is \Sigma, then the alphabet for \mathrm{MAKECS}(L) is \Sigma \cup \{\texttt{c},\texttt{s}\}.
UPDATE (2025-09-27): Though the problem is straightforwardly solvable as written, if it helps, you may assume that the alphabet for L does not contain c or s.
Consider the following language: B = \{w\mid w \textrm{ is a three digit number}\}
The alphabet for the language is \Sigma=\{\texttt{2},\texttt{4}\}. Prove that B is a regular language.
What is the language \mathrm{MAKECS}(B)? (answer must be a set)
Prove that \mathrm{MAKECS}(B) is a regular language
2 Are Regular Languages Closed Under \mathrm{MAKECS}?
Prove that the class of regular languages is closed under the \mathrm{MAKECS} operation.
In other words, prove if the input language L is a regular language, then \mathrm{MAKECS}(L) is a regular language.
Hint:
Give the equivalent IF-THEN statement that must be proved.
Give a proof of this IF-THEN statement.
Make sure your answer is in the form of a "Statements and Justifications" table, as explained in lecture (and also Hopcroft Chapter 1).
Since we dont know the input language L, if you need to give examples in your proof, you’ll need to express them in terms of the unknown input languages, e.g.:
"say we have a language L and string s_1\in L and s_2\notin L, then we know that ?? \in \mathrm{MAKECS}(L) and ??\notin \mathrm{MAKECS}(L)"
You should have at least 2 examples, which must include at least one that is in the output language and one that is not in the output language.
3 DFAs vs NFAs
Consider the diagram from Homework 1 DFA Formal Description:
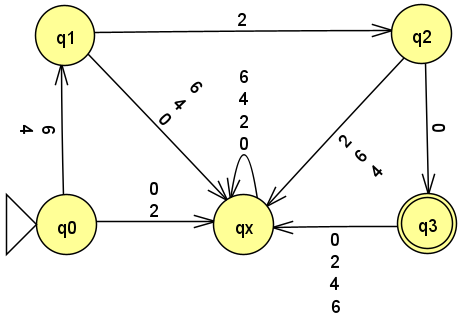
For this problem, assume the diagram is an NFA.
In class we learned that an NFA’s formal description has five components, e.g. N = (Q,\Sigma,\delta,q_{start},F), where \delta:Q\times\Sigma_\varepsilon\rightarrow\mathcal{P}(Q) is the transition function mapping a state and input symbol (or no symbol, in the case of an empty transition) to a set of states.
Come up with a formal NFA description of the diagram above (yes, it’s the same diagram as HW1, but now you are being told it an NFA).
Compare your answers from this problem and Homework 1 and give two differences between the formal description of a DFA and the formal description of an NFA.