Current Research Topics (constantly under construction)
Clustering and Characterization of Protein Intermediate Conformations
Exploring the conformational space of proteins can give us important information, such as the location and number of local minima, transition states, folding and binding related events etc. Since most sampling based search algorithms contain many random components, the conformational landscape has to be clustered and filtered in order to extract meaningful information. I have been working on several methods to cluster and characterize the conformational landscape of proteins. We showed a clustering method based on parallel coordinates and Gaussian mixture models, and argued that it is suited for providing information about the likelihood of the existence of given intermediate conformations in a protein conformational space. Parallel coordinates are a way of visualizing high-dimensional geometry and analyzing multivariate data. Dimensions or axes are laid out in parallel rather than orthogonal to each other. Each data value of an n-dimensional vector is positioned on the line corresponding to its axis, between the minimum (at the bottom) and the maximum (at the top) values of the axis. Points belonging to the same vector are connected by lines, which allows patterns between dimensions and outliers to be visually identified. For example, the following Figure shows a 5-dimensional data set displayed as a sequence of parallel coordinates.
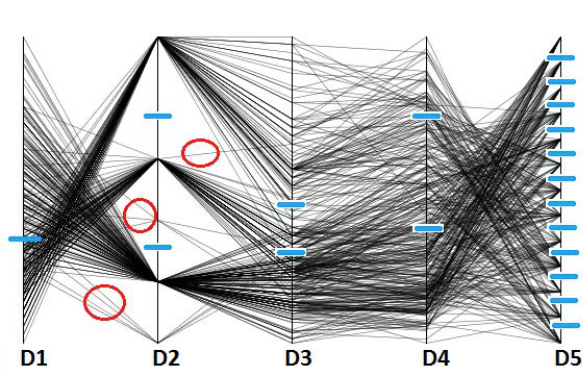
Our method analyzes the variance of each dimension to model those relations. The input is a lower-dimensional projection of a sampling of the conformational landscape of proteins. Each trajectory point is represented as a vector of some dimension n (usually between 5-20). In order to assign the clusters we first perform a model-based clustering on each dimension separately using Gaussian mixture distribution models to estimate density. A Gaussian or normal mixture model is a parametric probability density function represented as a weighted sum of Gaussian component densities.
In another study, done in collaboration with Dr. Eduardo Gonzalez from the Mathematics department, we used algebraic topology to characterize the conformational space of peptides and elucidate its topological properties. The method was used to find distinct energy minima while removing topological noise. This is done using persistent homology, which calculates homology groups at different resolutions to see which features persist for long periods of time. Informally, we can describe the process of computing the persistent homology as follows: The input a topological space X represented by a set of points in a certain Euclidean space - in our case a sampling of a low-energy subset of the conformations projected to some some lower-dimensional metric space. We define a ball of dimension N (the dimension of the data set) and radius epsilon around each point. In the beginning epsilon=0. As epsilon gradually increases, balls around points whose distances are <= 0.5 epsilon merge into one connected component as their balls intersect. If epsilon reaches half of the maximum distance between two points in the set, the entire set becomes one big ``blob''. Persistent homology finds properties of the space which persist as epsilon increases. It tries to find a value of epsilon which gives a good estimation of the topological properties of the space X, which can be expressed by Betti numbers. Intuitively, the Betti numbers of a space count the maximum number of cuts that can be made without dividing the space into two pieces. The kth Betti number refers to the number of unconnected k-dimensional surfaces. Therefore, the first three Betti numbers have the following intuitive definitions: b0 is the number of connected components, b1 is the number of two-dimensional or ``circular'' holes and b2 is the number of three-dimensional holes or ``voids''. A topological software package, JavaPlex yields barcodes associated to X, one for each separate k-dimensional surface, which are essentially given by the evolution of Betti numbers as epsilon increases. These barcodes are formally a set of intervals of the real line. A long line means that there is a component that persists as epsilon increases. All other smaller bars are not persistent and are considered topological noise. See figure:
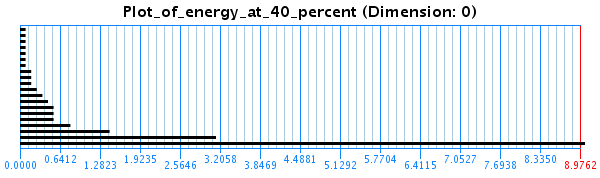
In this work we explore the conformational pathways of small peptides and larger proteins, emphasizing conformational clustering and detection of highly populated regions in the conformaitonal space, which could represent intermediate structures. Currently we are working on applying algorithms for robust dimensionality reduction. We are currently testing methods for robust PCA to try to reduce the noise, as well as Isomap, a non-linear dimensionality reduction methods which seem to give a better description of the conformational landscape of proteins . We tested Isomap and PCA on conformational trajectories from three different proteins that undergo large-scale changes using the sampling method described above. Our recent results show that Isomap produces compact, well-separated clusters and generally performs better than PCA. The results have recently been submitted to a journal, and the manuscript is currently under review. Current work includes testing our clustering method on Molecular Dynamics (MD) trajectories of short peptides to test the effect of the sampling method on the performance of our protocol.
Detecting Critical Regions in Proteins
Some regions in proteins play a critical role in determining their structure and function. Examples include flexible regions such as hinges which allow domain motion, and highly conserved functional interfaces which allow interactions with other proteins. Detecting these regions facilitates the analysis and simulation of protein rigidity and conformational changes, and aids in characterizing protein-protein binding. We work on analyzing critical residues in proteins using a combination of two complementary techniques. One method performs in-silico mutations and analyzes the protein's rigidity using graph-based techniques, to infer the role of a point substitution. The other method uses evolutionary conservation to find functional interfaces in proteins. We found, when testing our method on a set of experimentally known critical residues, that the two methods are able to detect more critical residues than each method separately. Our initial study suffered from a large number of false positives. In a later study we combined amino-acid specific information and data obtained by the two methods. We devised a machine learning model that combines both methods to a dataset of proteins with experimentally known critical residues, and were able to achieve a much higher prediction rate, more than either of the methods separately. Current work involves testing other classifiers such as propagation neural networks, and carefully verify our feature selection. We also apply our method to help detecting binding interfaces, which may aid in refinement of docked proteins. This work is done in collaboration with Dr. Filip Jagodzinski from Western Washington University.
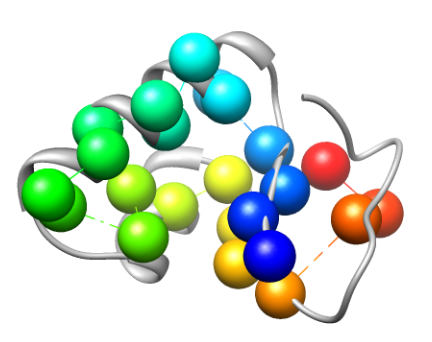
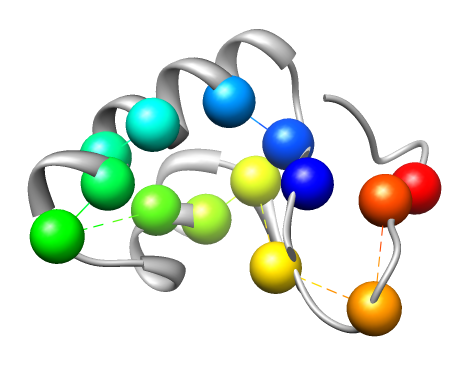
The cartoon rendering of the crystal structure of Crambin (PDB ID 1CRN) is colored in gray. Known critical residues based on experimental data (left) and critical residues detected by conservation analysis right)are depicted as spheres. Different colors represent different residues.
Docking and refinement using evolutionary information
Structural modeling of molecular assemblies lies at the heart of understanding molecular interactions and biological function. We present a method for docking protein molecules and elucidating native-like structures of protein dimers. We use geometric hashing to ensure the feasibility of searching the combined conformational space of dimeric structures. The search space is narrowed by focusing the sought rigid-body transformations around surface areas with evolutionary-conserved amino-acids. Recent analysis of protein assemblies reveals that many functional interfaces are significantly conserved throughout evolution. Our results show that focusing the search around evolutionary-conserved interfaces results in lower lRMSDs.
However, computational docking methods are often not accurate and their results need to be further refined to improve interface packing. We introduce a novel refinement method that incorporates evolutionary information by employing an energy function containing Evolutionary Trace (ET)-based scoring function, which also takes shape complementarity, electrostatic and Van der Waals interactions into account. Our refinement method is able to produce structures with better RMSDs with respect to the known complexes and lower energies than those initial docked structures. Most recent work involves developing neural network based classifiers to predict and refine docked complexes
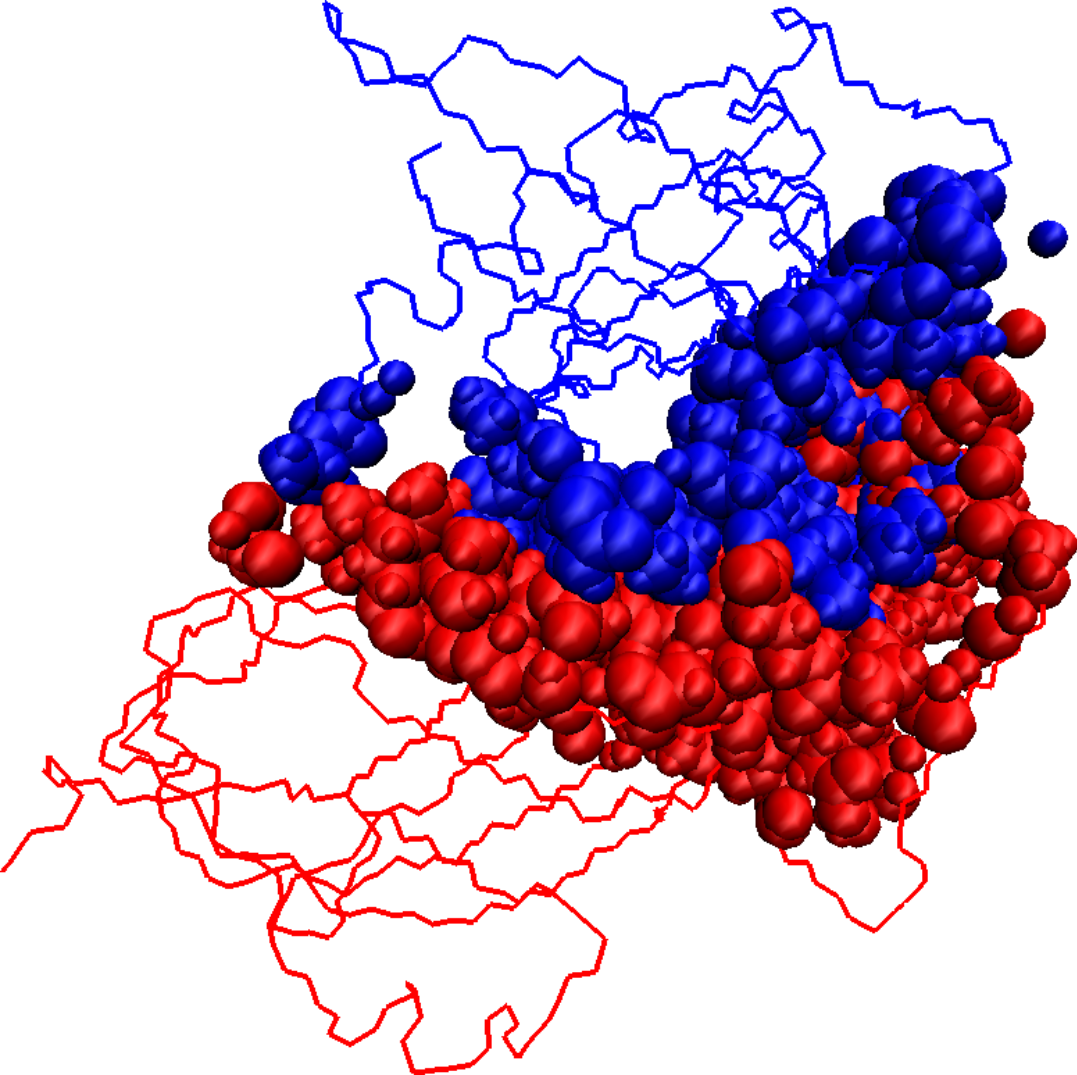
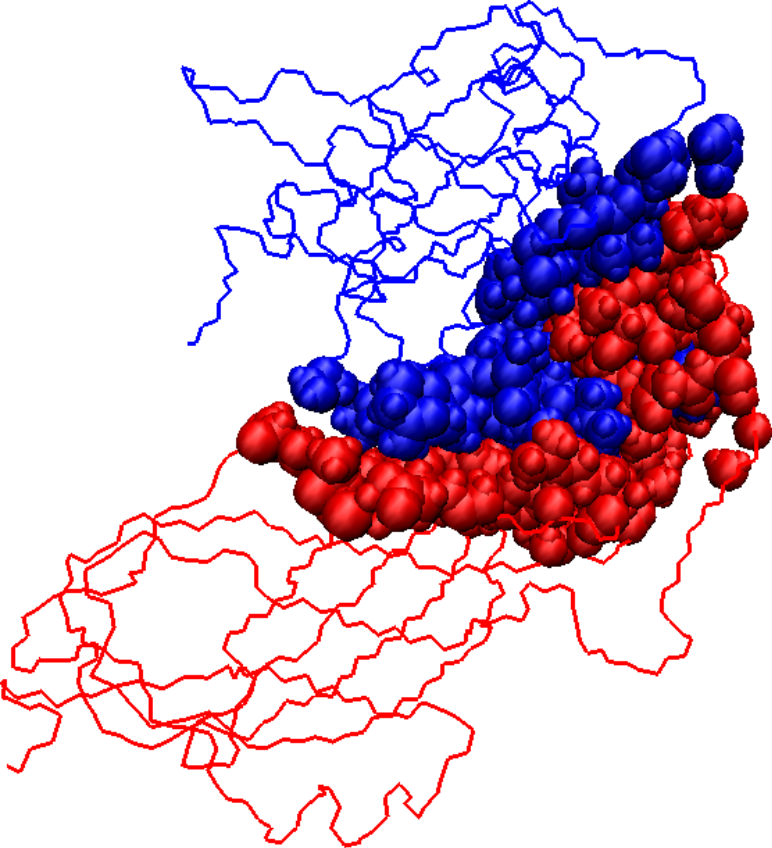
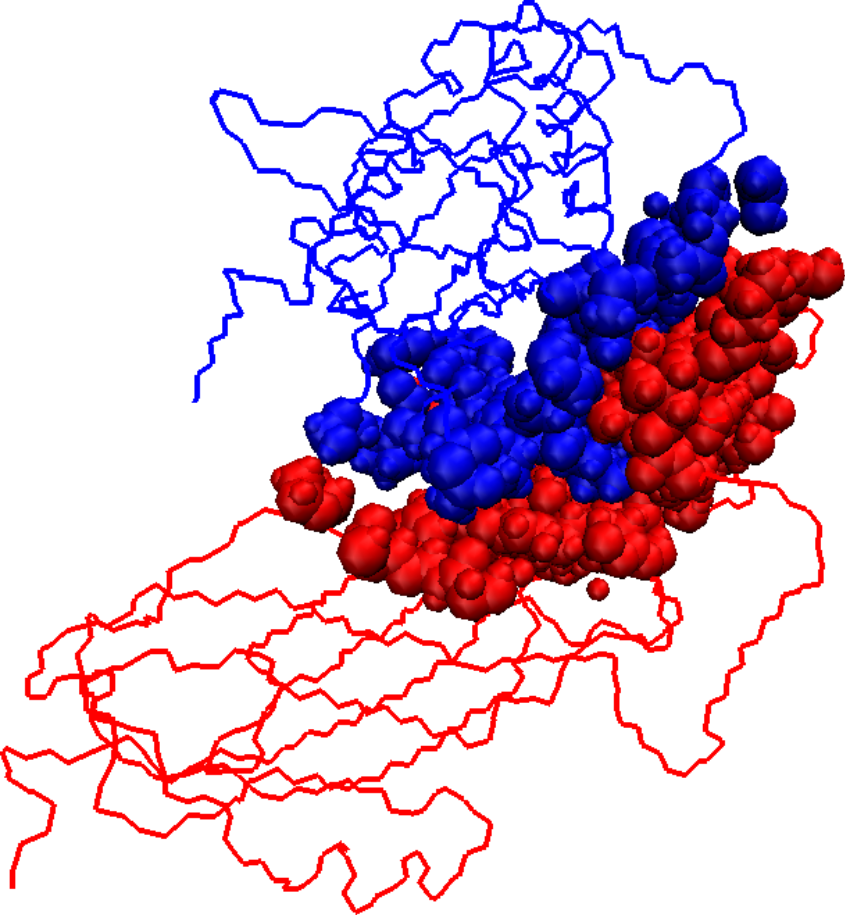
Initial docked solution for 1DS6 has 1546 interface atoms (a), the refined version of the initial docked solution has 1125 interface atoms (b), and the native structure for 1DS6 has 976 interface atoms (c). Interface atoms are drawn as spheres. Chain A is colored in blue and chain B in red.
Characterizing protein-protein and protein-ligand interactions
Neuropilin-1 (NRP-1) is a hub receptor that plays an essential role in angiogenesis, vascular permeability and nervous system development. Previous studies have shown that peptides with an N-terminal Arg, especially peptides expressing the consensus sequence R/K/XXR/K, were expressed in phage libraries expressing peptides for binding to prostate cancer cells. These sequences promoted binding and internalization into tumor cells, while blocking the C-terminal Arg (or Lys) prevented internalization. Such peptides were shown to bind strongly to NRP-1 on the target cells. In this study we investigate the properties of the complex that results from binding of NRP-1 to one of those peptides, RPAR, and perform computational mutant study in order to study the physical, chemical and structural properties of the bound complex and suggest variants that may increase complex binding.
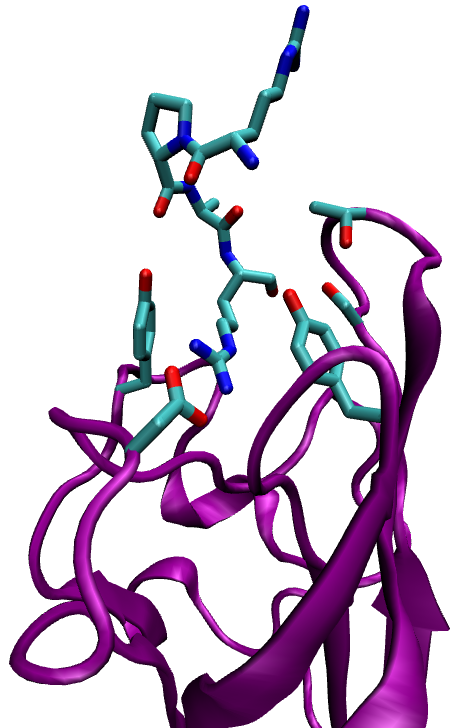
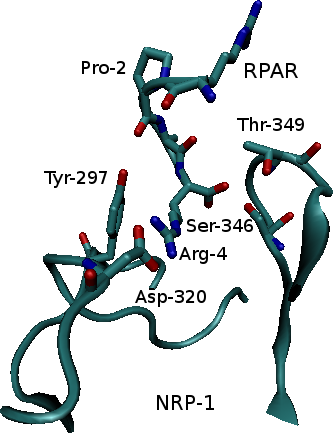
Ribbon representation of the NRP-1 - RPAR complex (left) and a closeup on the binding site (right). Interacting residues are labeled.
Nano-design of novel structures based on functional amyloids and polymer motifs
In this work we elucidate the conformational preferences of two amyloid-forming peptides, Arginine-Vasopressin and Neuromedin-K, and two new biomacromolecular conjugates obtained by linking the two peptides to a polyester (poly(R-lactic acid)) chain. The conformational properties of the new hybrid conjugates are assessed through molecular dynamics simulations and compared to those of their individual components. Our results suggest that the free unconjugated peptides tend to adopt backbone arrangements which resemble a beta-hairpin shape, a conformation which has been reported to facilitate amyloid self-aggregation. The backbone conformational preferences of the unlinked peptides are maintained in the peptide-polymer hybrid. Yet significant differences in the side-chains nonbonding interactions patterns were detected between the two states. This suggests that the conformational profile of the peptides' backbones is preserved when linked to the polymer, maintaining the amyloid precursor-like structure. Our results provide a conformational exploration of two amyloid-forming peptides and first steps toward the design of two feasible self-aggregating hybrid materials.