Homework 10🔗

Last updated: Mon, 10 Nov 2025 12:06:32 -0500

Out: Mon Nov 10, 12:00pm EDT (noon) Due: Mon Nov 17, 12:00pm EDT (noon)

Note: Assignments are not officially "released" until—and are subject to change without notice up to—the indicated "Out" date and time. If an assignment is posted early, students may look ahead but are responsible for ensuring that they are always working with the most recent version of the homework.

This assignment continues to explore Turing machines, specifically deciders.

Homework Problems

1. A Decidable Language (15 points)

2. A Language of DFAs (15 points)

3. Context-free Languages vs Turing-recognizable Languages (16 points)

4. Chomsky Normal Form for CFGs (14 points)

5. README (2 point)

Total: 62 points

Submitting

Submit your solution to this assignment in Gradescope hw10. Please assign each page to the correct problem and make sure your solutions are legible.

A submission must also include a README containing the required information.

1 A Decidable Language🔗

Prove that the following language is a decidable language:

L_{AC} = \{w\mid w\textrm{ is a valid area code}\}

You may assume that strings in the language are drawn from alphabet \{\texttt{2},\texttt{3},\texttt{4}\}, and that valid area codes are any three digit number made up of characters from the alphabet.

If your answer involves a decider, its definition must include a termination argument.

Also, for this problem, the decider must use at least one machine we have previously defined in lecture or homework. (Remember that when creating new Turing machines, all other machines or algorithms previously constructed in class or in previous homeworks are available as a "library"!)

Finally, make sure your proof includes the necessary Examples Table with the appropriate columns (e.g., whether strings are in the language, whether strings are accepted by the decider, existing machines used, etc.).

2 A Language of DFAs🔗

Prove that the following language is a decidable language:

\textrm{NONAC}_{\textsf{DFA}} = \left\{\left\langle D\right\rangle\mid D\textrm{ is a DFA that accepts all numbers except area codes}\right\}

You may assume that strings in the language are drawn from alphabet \{\texttt{2},\texttt{3},\texttt{4}\}, and that valid area codes are any three digit number made up of characters from the alphabet.

If your answer involves a decider, its definition must include a termination argument.

Also, for this problem, the decider must use at least two machine we have previously defined in lecture or homework. (Remember that when creating new Turing machines, all other machines or algorithms previously constructed in class or in previous homeworks are available as a "library"!)

Finally, make sure your proof includes the necessary Examples Table with the appropriate columns (e.g., whether strings are in the language, whether strings are accepted by the decider, existing machines used, etc.).

3 Context-free Languages vs Turing-recognizable Languages🔗

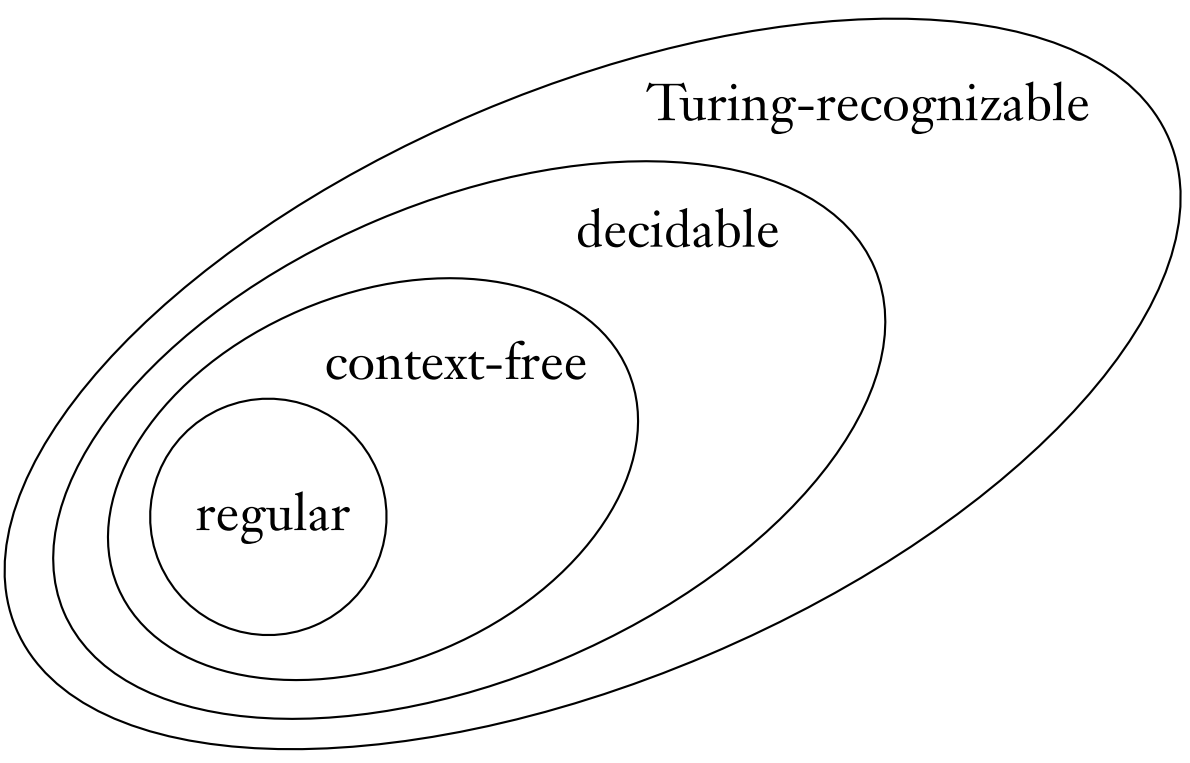
Prove that the "context-free" and "Turing-recognizable" ovals in the language Venn Diagram from class are "correct" with respect to each other.

4 Chomsky Normal Form for CFGs🔗

Recall that a CFG is in Chomsky Normal Form (CNF) if all rules have the form:

where \texttt{a} must be a terminal, A, B, C are variables, and B and C are not the start variable.

In addition, a grammar in CNF may include a rule A\rightarrow \varepsilon if A is the start variable.

Convert the following context-free grammar to Chomsky Normal Form using the algorithm described in class.

• S\rightarrow XY

• X\rightarrow \texttt{b}X\mid\varepsilon

• Y\rightarrow \texttt{c}Y\texttt{d}\mid \varepsilon

The start variable of the CFG is S and the set of terminals is \{\texttt{b},\texttt{c},\texttt{d}\}